Question Number 92423 by mhmd last updated on 06/May/20
![lim_(x⇒∞) ((4(x+3)!−x!)/(x[(x+2)!−(x−1)!]))](https://www.tinkutara.com/question/Q92423.png)
$${lim}_{{x}\Rightarrow\infty} \frac{\mathrm{4}\left({x}+\mathrm{3}\right)!−{x}!}{{x}\left[\left({x}+\mathrm{2}\right)!−\left({x}−\mathrm{1}\right)!\right]} \\ $$
Answered by john santu last updated on 07/May/20
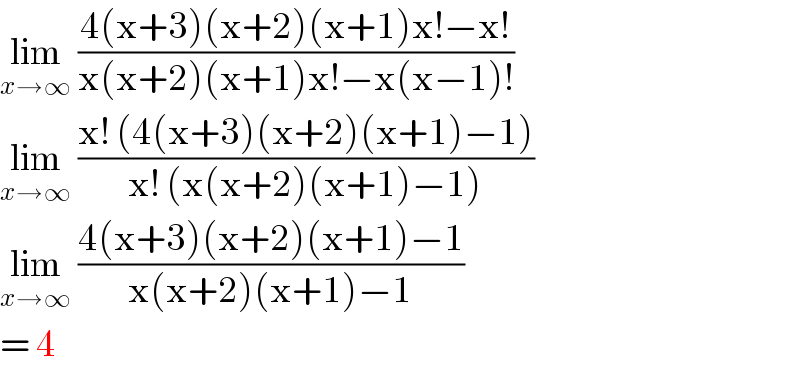
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{4}\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{1}\right)\mathrm{x}!−\mathrm{x}!}{\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{1}\right)\mathrm{x}!−\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)!} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{x}!\:\left(\mathrm{4}\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{1}\right)}{\mathrm{x}!\:\left(\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{1}\right)} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{4}\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{1}} \\ $$$$=\:\mathrm{4}\: \\ $$
