Question Number 168004 by mathlove last updated on 31/Mar/22
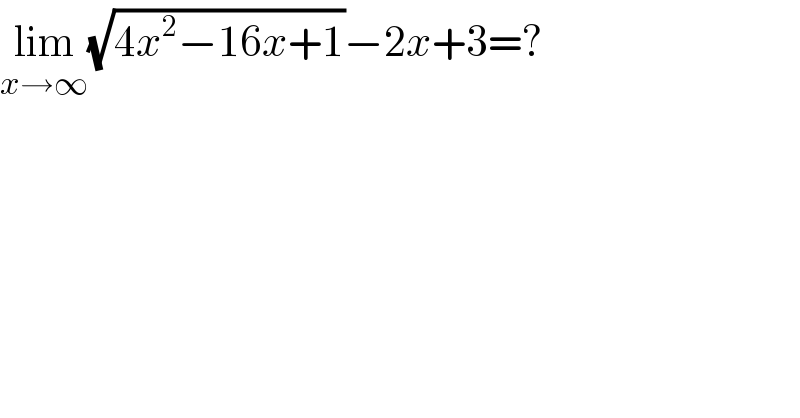
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}}−\mathrm{2}{x}+\mathrm{3}=? \\ $$
Answered by nurtani last updated on 31/Mar/22
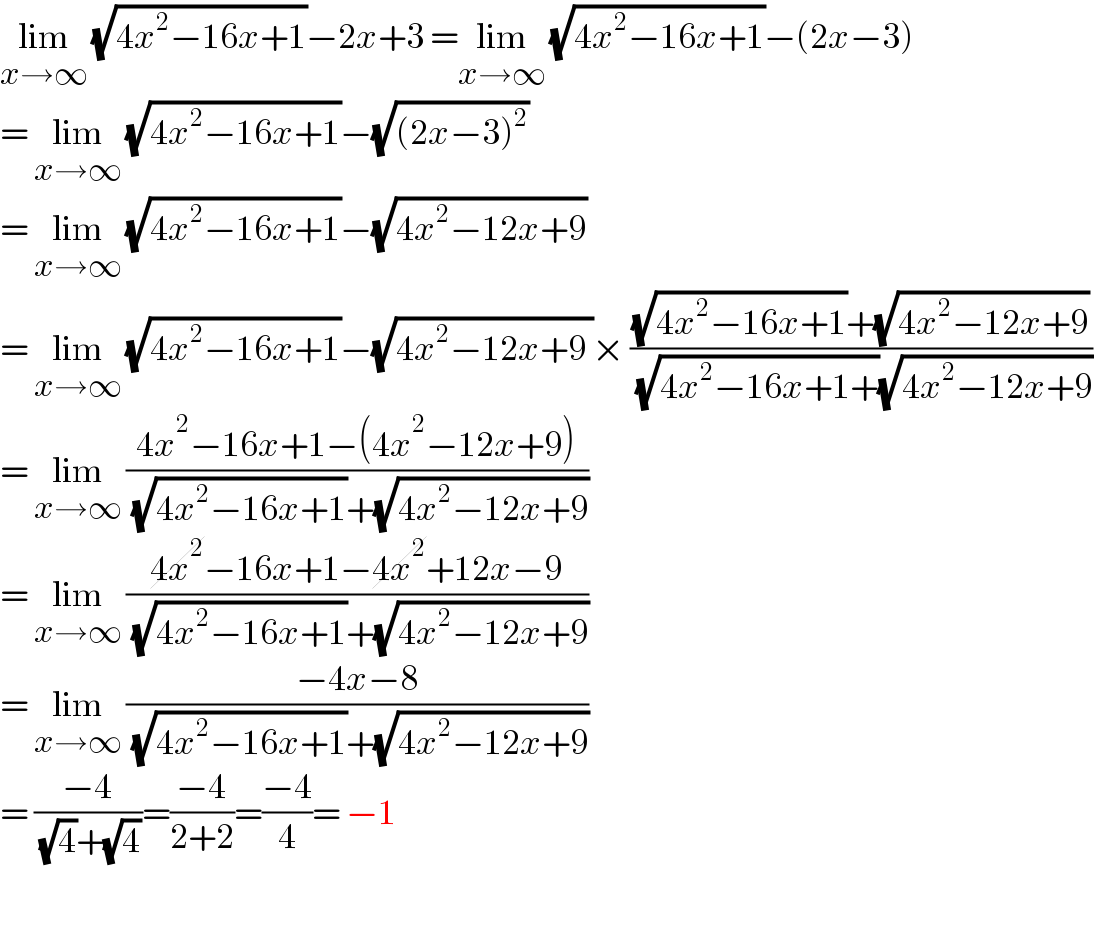
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}}−\mathrm{2}{x}+\mathrm{3}\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}}−\left(\mathrm{2}{x}−\mathrm{3}\right) \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}}−\sqrt{\left(\mathrm{2}{x}−\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}}−\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{9}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}}−\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{9}\:}×\:\frac{\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}}+\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{9}}}{\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}+}\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{9}}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}−\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{9}\right)}{\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}}+\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{9}}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\cancel{\mathrm{4}{x}^{\mathrm{2}} }−\mathrm{16}{x}+\mathrm{1}−\cancel{\mathrm{4}{x}^{\mathrm{2}} }+\mathrm{12}{x}−\mathrm{9}}{\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}}+\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{9}}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{−\mathrm{4}{x}−\mathrm{8}}{\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{1}}+\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{9}}} \\ $$$$=\:\frac{−\mathrm{4}}{\:\sqrt{\mathrm{4}}+\sqrt{\mathrm{4}}}=\frac{−\mathrm{4}}{\mathrm{2}+\mathrm{2}}=\frac{−\mathrm{4}}{\mathrm{4}}=\:−\mathrm{1} \\ $$$$ \\ $$
Commented by mathlove last updated on 31/Mar/22

$${thanks} \\ $$
