lim-x-5-x-5-2-cot-2-2-x-5-

Question Number 96977 by 175 last updated on 05/Jun/20

\lim_{x \to 5} \frac{x - 5}{2 + \cot^{2} \frac{2}{x - 5}}

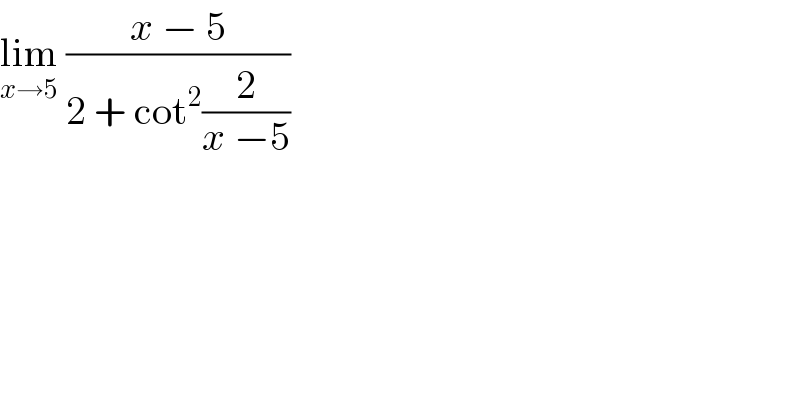
Answered by mathmax by abdo last updated on 06/Jun/20

let f (x) = \frac{x - 5}{2 + \frac{1}{\tan^{2} (\frac{2}{x - 5})}} changement x - 5 = t give f (x) = g (t)

= \frac{t}{2 + \frac{1}{\tan^{2} (\frac{2}{t})}} = \frac{{ttan}^{2} (\frac{2}{t})}{{2 \tan}^{2} (\frac{2}{t}) + 1} (x \to 5 \Rightarrow t \to 0)

g (t) = \frac{{tsin}^{2} (\frac{2}{t})}{{2 \sin}^{2} (\frac{2}{t}) + \cos^{2} (\frac{2}{t})} = \frac{{tsin}^{2} (\frac{2}{t})}{1 + \sin^{2} (\frac{2}{t})}

0 ⩽ \sin^{2} (\frac{2}{t}) ⩽ 1 \Rightarrow 1 ⩽ 1 + \sin^{2} (\frac{2}{t}) ⩽ 2 \Rightarrow \frac{1}{2} ⩽ \frac{1}{1 + \sin^{2} (\frac{2}{t})} ⩽ 1 \Rightarrow

\frac{∣ t ∣}{2} ⩽∣ g (t) ∣⩽∣ t ∣ \to 0 (t \to 0) \Rightarrow \lim_{x \to 0} g (t) = 0 = \lim_{x \to 5} f (x) .

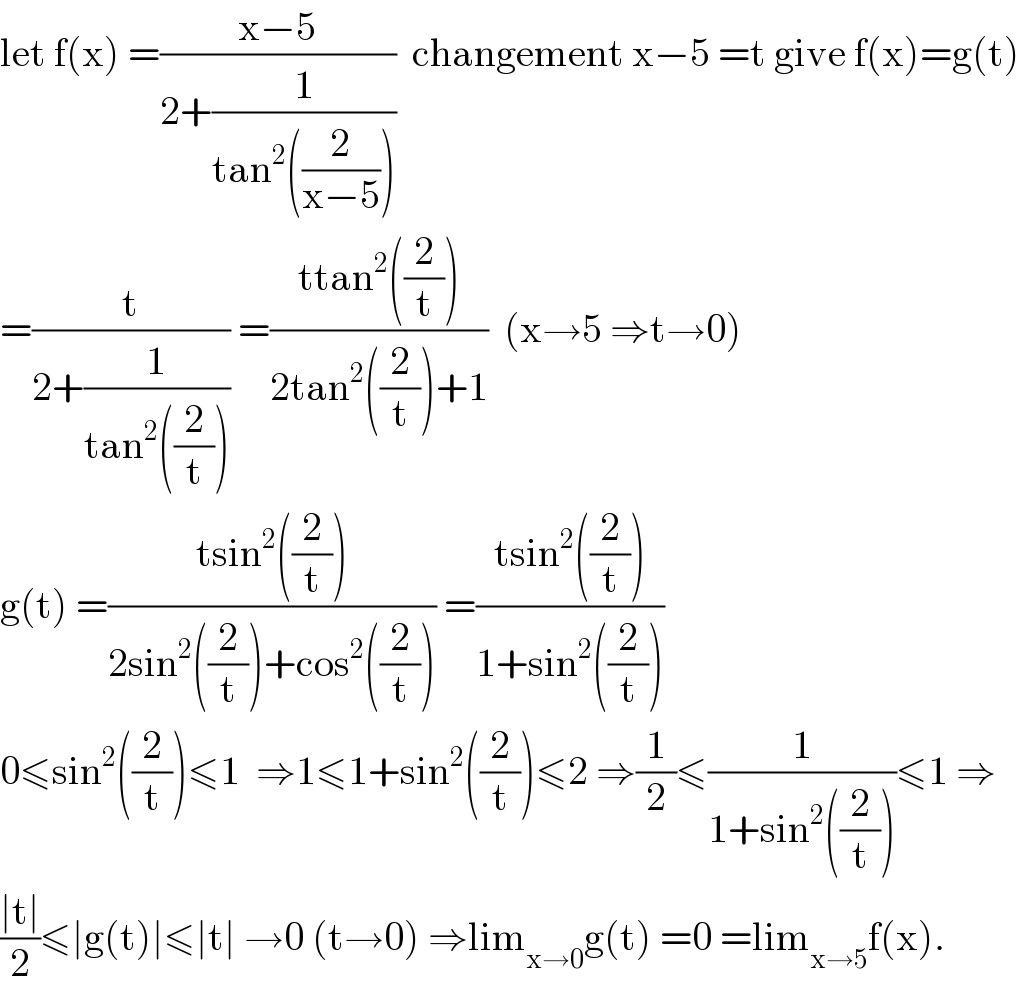
Commented by 175 last updated on 06/Jun/20

you are a great mathematical thanks alot

Commented by abdomathmax last updated on 06/Jun/20

you are welcome sir .