Question Number 96931 by bobhans last updated on 05/Jun/20
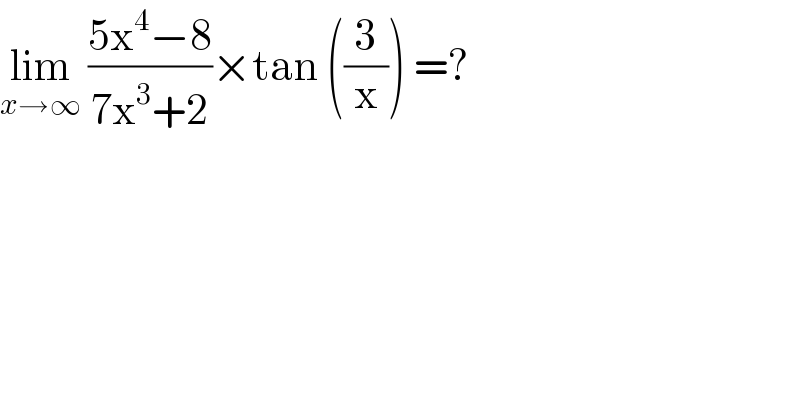
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{5x}^{\mathrm{4}} −\mathrm{8}}{\mathrm{7x}^{\mathrm{3}} +\mathrm{2}}×\mathrm{tan}\:\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\:=? \\ $$
Commented by PRITHWISH SEN 2 last updated on 05/Jun/20
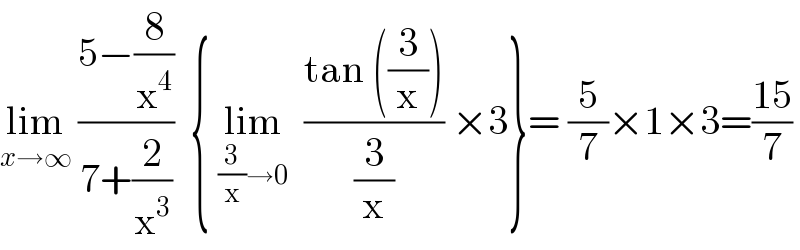
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{5}−\frac{\mathrm{8}}{\mathrm{x}^{\mathrm{4}} }}{\mathrm{7}+\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }}\:\:\left\{\:\underset{\frac{\mathrm{3}}{\mathrm{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{tan}\:\left(\frac{\mathrm{3}}{\mathrm{x}}\right)}{\frac{\mathrm{3}}{\mathrm{x}}}\:×\mathrm{3}\right\}=\:\frac{\mathrm{5}}{\mathrm{7}}×\mathrm{1}×\mathrm{3}=\frac{\mathrm{15}}{\mathrm{7}} \\ $$
Commented by bemath last updated on 06/Jun/20
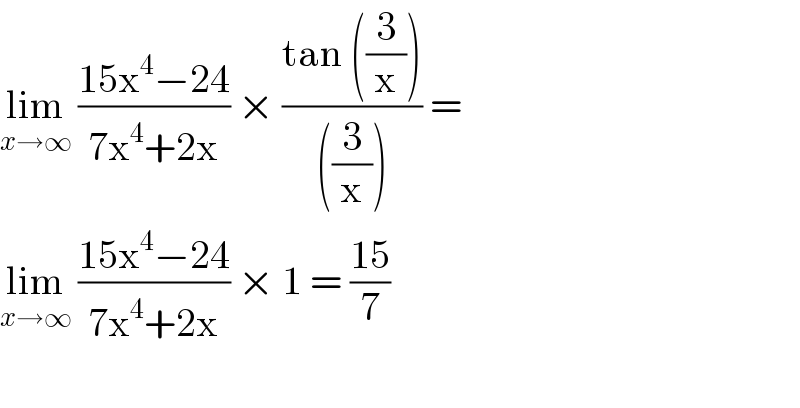
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{15x}^{\mathrm{4}} −\mathrm{24}}{\mathrm{7x}^{\mathrm{4}} +\mathrm{2x}}\:×\:\frac{\mathrm{tan}\:\left(\frac{\mathrm{3}}{\mathrm{x}}\right)}{\left(\frac{\mathrm{3}}{\mathrm{x}}\right)}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{15x}^{\mathrm{4}} −\mathrm{24}}{\mathrm{7x}^{\mathrm{4}} +\mathrm{2x}}\:×\:\mathrm{1}\:=\:\frac{\mathrm{15}}{\mathrm{7}} \\ $$$$ \\ $$
Commented by bobhans last updated on 06/Jun/20

$$\mathrm{yes}..\mathrm{thanks}\:\mathrm{all} \\ $$
Answered by RAMANA last updated on 05/Jun/20
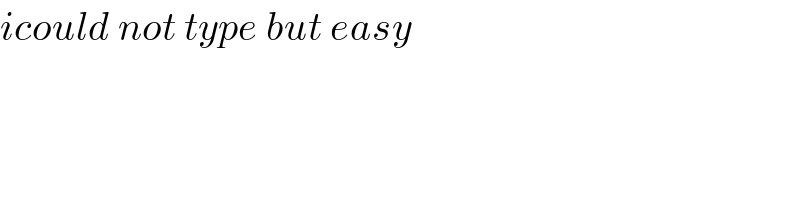
$${icould}\:{not}\:{type}\:{but}\:{easy} \\ $$
Answered by 1549442205 last updated on 05/Jun/20
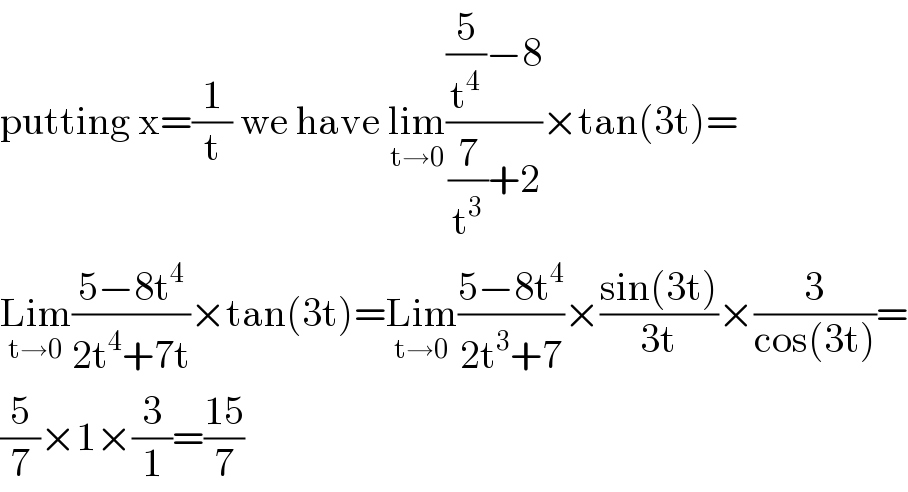
$$\mathrm{putting}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\:\mathrm{we}\:\mathrm{have}\:\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{5}}{\mathrm{t}^{\mathrm{4}} }−\mathrm{8}}{\frac{\mathrm{7}}{\mathrm{t}^{\mathrm{3}} }+\mathrm{2}}×\mathrm{tan}\left(\mathrm{3t}\right)= \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{Lim}}\frac{\mathrm{5}−\mathrm{8t}^{\mathrm{4}} }{\mathrm{2t}^{\mathrm{4}} +\mathrm{7t}}×\mathrm{tan}\left(\mathrm{3t}\right)=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{Lim}}\frac{\mathrm{5}−\mathrm{8t}^{\mathrm{4}} }{\mathrm{2t}^{\mathrm{3}} +\mathrm{7}}×\frac{\mathrm{sin}\left(\mathrm{3t}\right)}{\mathrm{3t}}×\frac{\mathrm{3}}{\mathrm{cos}\left(\mathrm{3t}\right)}= \\ $$$$\frac{\mathrm{5}}{\mathrm{7}}×\mathrm{1}×\frac{\mathrm{3}}{\mathrm{1}}=\frac{\mathrm{15}}{\mathrm{7}} \\ $$
