Question Number 61791 by naka3546 last updated on 08/Jun/19
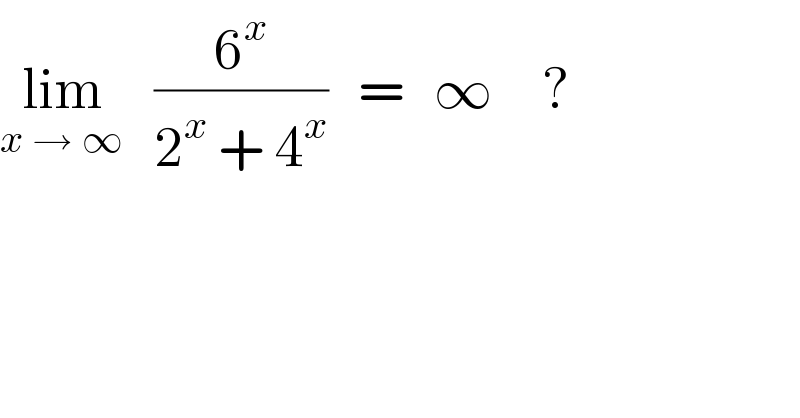
$$\underset{{x}\:\rightarrow\:\infty} {\mathrm{lim}}\:\:\:\frac{\mathrm{6}^{{x}} }{\mathrm{2}^{{x}} \:+\:\mathrm{4}^{{x}} }\:\:\:=\:\:\:\infty\:\:\:\:\:? \\ $$
Commented by mr W last updated on 08/Jun/19
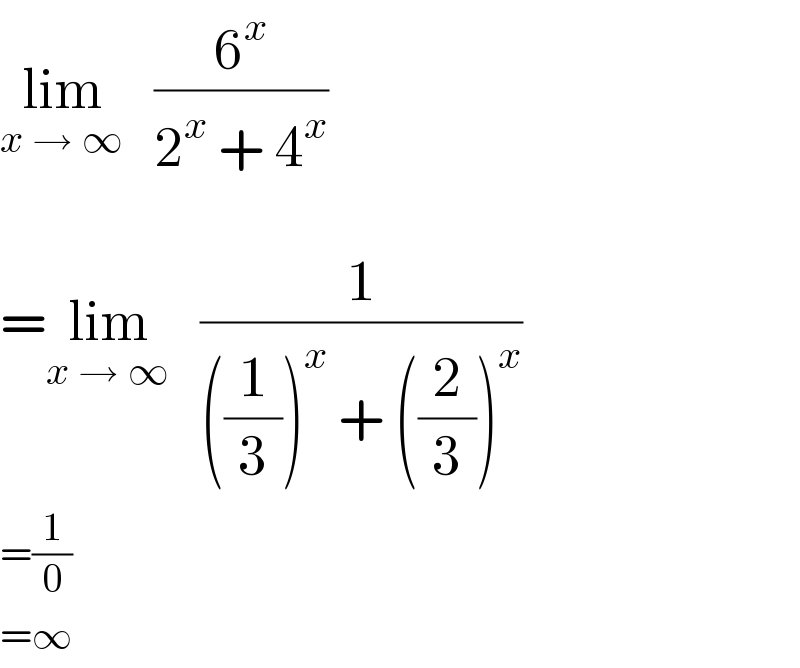
$$\underset{{x}\:\rightarrow\:\infty} {\mathrm{lim}}\:\:\:\frac{\mathrm{6}^{{x}} }{\mathrm{2}^{{x}} \:+\:\mathrm{4}^{{x}} } \\ $$$$ \\ $$$$=\underset{{x}\:\rightarrow\:\infty} {\mathrm{lim}}\:\:\:\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{x}} \:+\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{0}} \\ $$$$=\infty \\ $$
Answered by JDamian last updated on 08/Jun/19
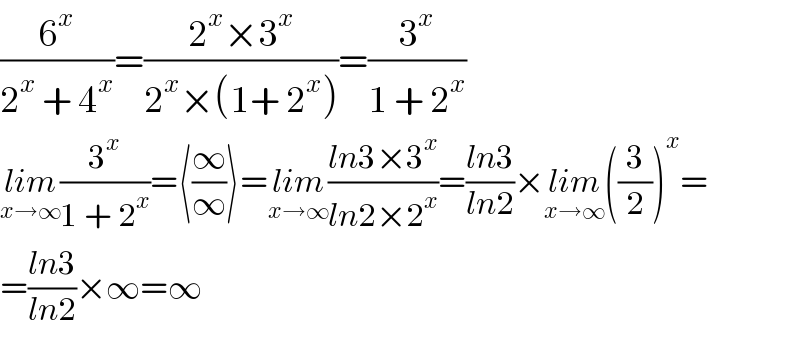
$$\frac{\mathrm{6}^{{x}} }{\mathrm{2}^{{x}} \:+\:\mathrm{4}^{{x}} }=\frac{\mathrm{2}^{{x}} ×\mathrm{3}^{{x}} }{\mathrm{2}^{{x}} ×\left(\mathrm{1}+\:\mathrm{2}^{{x}} \right)}=\frac{\mathrm{3}^{{x}} }{\mathrm{1}\:+\:\mathrm{2}^{{x}} } \\ $$$$\underset{{x}\rightarrow\infty} {{lim}}\frac{\mathrm{3}^{{x}} }{\mathrm{1}\:+\:\mathrm{2}^{{x}} }=\langle\frac{\infty}{\infty}\rangle=\underset{{x}\rightarrow\infty} {{lim}}\frac{{ln}\mathrm{3}×\mathrm{3}^{{x}} }{{ln}\mathrm{2}×\mathrm{2}^{{x}} }=\frac{{ln}\mathrm{3}}{{ln}\mathrm{2}}×\underset{{x}\rightarrow\infty} {{lim}}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{x}} = \\ $$$$=\frac{{ln}\mathrm{3}}{{ln}\mathrm{2}}×\infty=\infty \\ $$
