Question Number 92966 by i jagooll last updated on 10/May/20
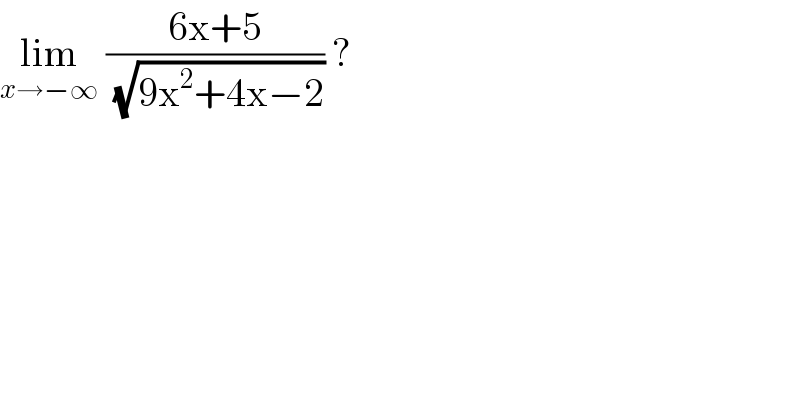
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{6x}+\mathrm{5}}{\:\sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{4x}−\mathrm{2}}}\:? \\ $$
Commented by i jagooll last updated on 10/May/20
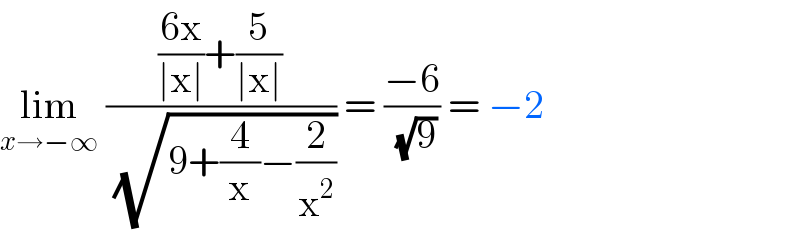
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\frac{\mathrm{6x}}{\mid\mathrm{x}\mid}+\frac{\mathrm{5}}{\mid\mathrm{x}\mid}}{\:\sqrt{\mathrm{9}+\frac{\mathrm{4}}{\mathrm{x}}−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }}}\:=\:\frac{−\mathrm{6}}{\:\sqrt{\mathrm{9}}}\:=\:−\mathrm{2} \\ $$
Commented by abdomathmax last updated on 10/May/20
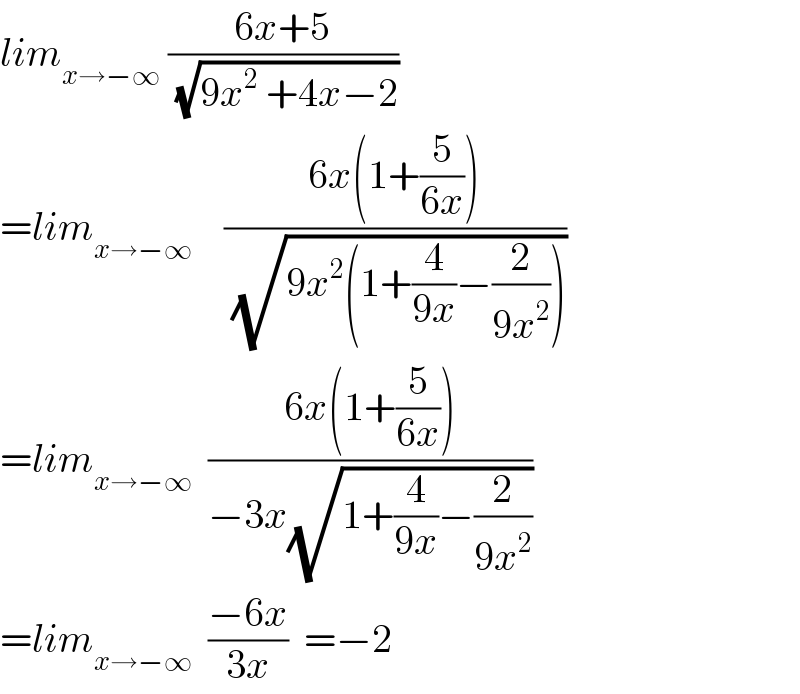
$${lim}_{{x}\rightarrow−\infty} \:\frac{\mathrm{6}{x}+\mathrm{5}}{\:\sqrt{\mathrm{9}{x}^{\mathrm{2}} \:+\mathrm{4}{x}−\mathrm{2}}} \\ $$$$={lim}_{{x}\rightarrow−\infty} \:\:\:\:\frac{\mathrm{6}{x}\left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{6}{x}}\right)}{\:\sqrt{\mathrm{9}{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{9}{x}}−\frac{\mathrm{2}}{\mathrm{9}{x}^{\mathrm{2}} }\right)}} \\ $$$$={lim}_{{x}\rightarrow−\infty} \:\:\frac{\mathrm{6}{x}\left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{6}{x}}\right)}{−\mathrm{3}{x}\sqrt{\mathrm{1}+\frac{\mathrm{4}}{\mathrm{9}{x}}−\frac{\mathrm{2}}{\mathrm{9}{x}^{\mathrm{2}} }}} \\ $$$$={lim}_{{x}\rightarrow−\infty} \:\:\frac{−\mathrm{6}{x}}{\mathrm{3}{x}}\:\:=−\mathrm{2} \\ $$
Commented by i jagooll last updated on 10/May/20
cool man ☺☺☺
