Question Number 163582 by mathlove last updated on 08/Jan/22
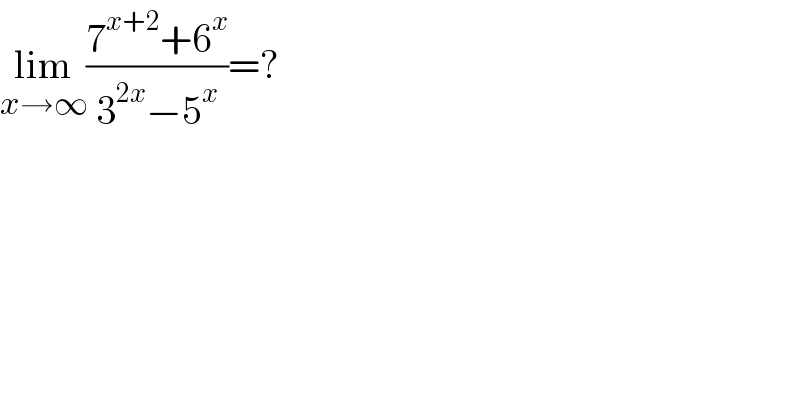
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{7}^{{x}+\mathrm{2}} +\mathrm{6}^{{x}} }{\mathrm{3}^{\mathrm{2}{x}} −\mathrm{5}^{{x}} }=? \\ $$
Answered by cortano1 last updated on 08/Jan/22
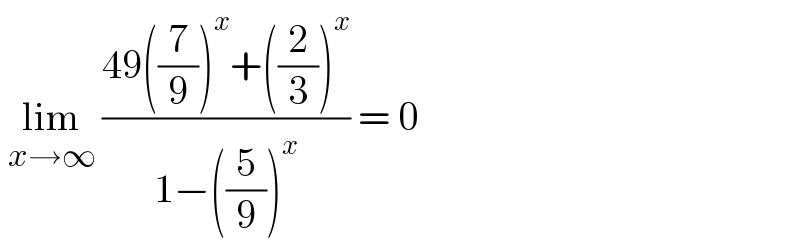
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{49}\left(\frac{\mathrm{7}}{\mathrm{9}}\right)^{{x}} +\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} }{\mathrm{1}−\left(\frac{\mathrm{5}}{\mathrm{9}}\right)^{{x}} }\:=\:\mathrm{0} \\ $$
Commented by mathlove last updated on 09/Jan/22

$$ \\ $$If given a little explanation
