Question Number 50089 by Cheyboy last updated on 13/Dec/18
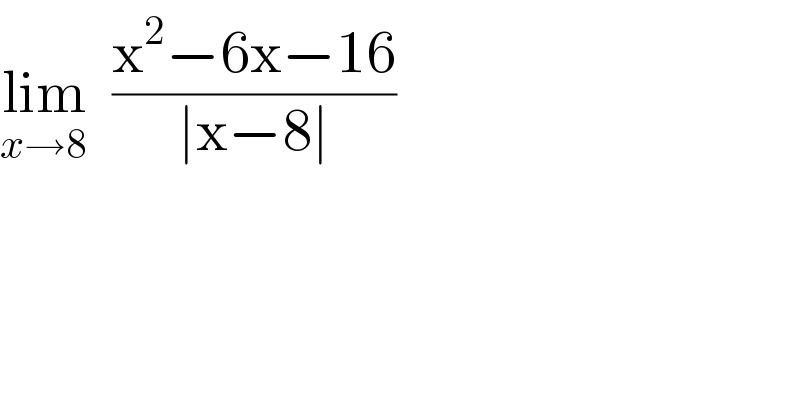
$$\underset{{x}\rightarrow\mathrm{8}} {\mathrm{lim}}\:\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{6x}−\mathrm{16}}{\mid\mathrm{x}−\mathrm{8}\mid} \\ $$
Commented by Abdo msup. last updated on 14/Dec/18
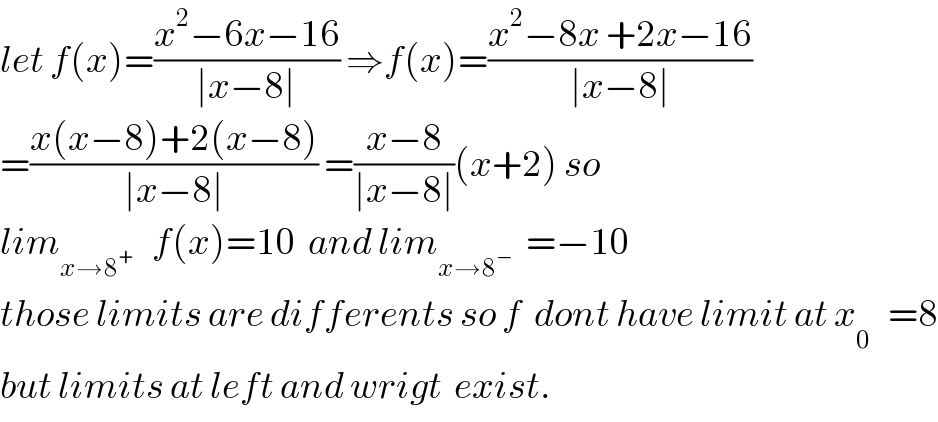
$${let}\:{f}\left({x}\right)=\frac{{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{16}}{\mid{x}−\mathrm{8}\mid}\:\Rightarrow{f}\left({x}\right)=\frac{{x}^{\mathrm{2}} −\mathrm{8}{x}\:+\mathrm{2}{x}−\mathrm{16}}{\mid{x}−\mathrm{8}\mid} \\ $$$$=\frac{{x}\left({x}−\mathrm{8}\right)+\mathrm{2}\left({x}−\mathrm{8}\right)}{\mid{x}−\mathrm{8}\mid}\:=\frac{{x}−\mathrm{8}}{\mid{x}−\mathrm{8}\mid}\left({x}+\mathrm{2}\right)\:{so} \\ $$$${lim}_{{x}\rightarrow\mathrm{8}^{+} } \:\:\:{f}\left({x}\right)=\mathrm{10}\:\:{and}\:{lim}_{{x}\rightarrow\mathrm{8}^{−} } \:\:=−\mathrm{10} \\ $$$${those}\:{limits}\:{are}\:{differents}\:{so}\:{f}\:\:{dont}\:{have}\:{limit}\:{at}\:{x}_{\mathrm{0}^{} } \:\:=\mathrm{8} \\ $$$${but}\:{limits}\:{at}\:{left}\:{and}\:{wrigt}\:\:{exist}. \\ $$
Commented by Cheyboy last updated on 14/Dec/18

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{guyz} \\ $$
Answered by ajfour last updated on 13/Dec/18
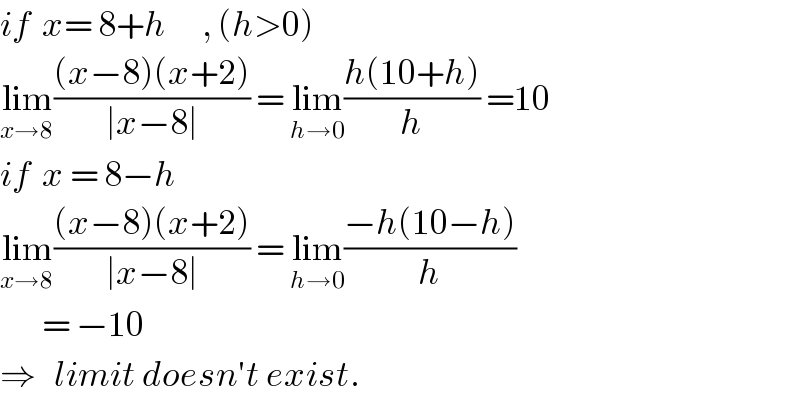
$${if}\:\:{x}=\:\mathrm{8}+{h}\:\:\:\:\:\:,\:\left({h}>\mathrm{0}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{8}} {\mathrm{lim}}\frac{\left({x}−\mathrm{8}\right)\left({x}+\mathrm{2}\right)}{\mid{x}−\mathrm{8}\mid}\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{h}\left(\mathrm{10}+{h}\right)}{{h}}\:=\mathrm{10} \\ $$$${if}\:\:{x}\:=\:\mathrm{8}−{h} \\ $$$$\underset{{x}\rightarrow\mathrm{8}} {\mathrm{lim}}\frac{\left({x}−\mathrm{8}\right)\left({x}+\mathrm{2}\right)}{\mid{x}−\mathrm{8}\mid}\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−{h}\left(\mathrm{10}−{h}\right)}{{h}} \\ $$$$\:\:\:\:\:\:\:=\:−\mathrm{10} \\ $$$$\Rightarrow\:\:\:{limit}\:{doesn}'{t}\:{exist}. \\ $$
