Menu Close

lim-x-8x-3-4x-2-1-1-3-8x-3-px-2-1-1-3-1-4-find-p-

Tinku Tara 0 Comments
Pin




Question Number 82175 by jagoll last updated on 19/Feb/20
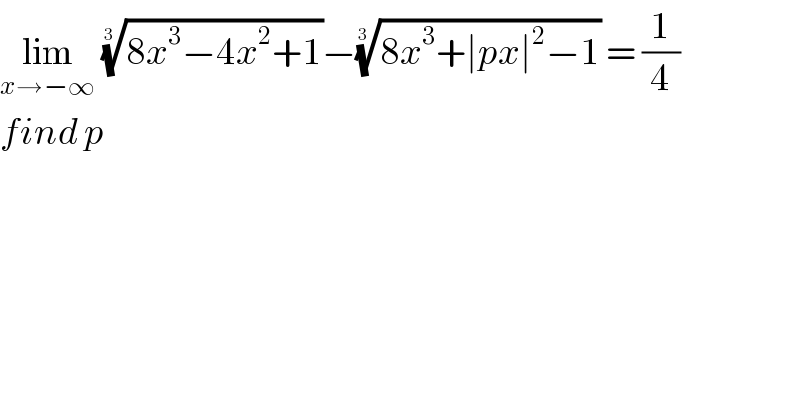
lim_(x→−∞) ((8x^3 −4x^2 +1))^(1/(3 )) −((8x^3 +∣px∣^2 −1))^(1/(3 )) = (1/4) find p
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{3}\:}]{\mathrm{8}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}}−\sqrt[{\mathrm{3}\:}]{\mathrm{8}{x}^{\mathrm{3}} +\mid{px}\mid^{\mathrm{2}} −\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${find}\:{p}\: \\ $$
Commented by mr W last updated on 19/Feb/20
please check sir! question is wrong. the limit is ≤−(1/3). it can neither be (1/4) nor −(1/4).
$${please}\:{check}\:{sir}! \\ $$$${question}\:{is}\:{wrong}.\:{the}\:{limit}\:{is}\:\leqslant−\frac{\mathrm{1}}{\mathrm{3}}. \\ $$$${it}\:{can}\:{neither}\:{be}\:\frac{\mathrm{1}}{\mathrm{4}}\:{nor}\:−\frac{\mathrm{1}}{\mathrm{4}}. \\ $$
Commented by john santu last updated on 19/Feb/20
lim_(u→0^− ) ((((8−4u+u^3 ))^(1/(3 )) − ((8+∣p∣ u−u^3 ))^(1/(3 )) )/u) = lim_(u→0^− ) ((((3u^2 −4)/(3((((8−4u+u^3 )^2 ))^(1/(3 )) ))− (((−3u^2 +∣p∣))/(3((((8+∣p∣u−u^3 )^2 ))^(1/(3 )) )))/1) = ((−4)/(3.4))−((∣p∣)/(3.4)) = (1/4) ⇒ −(1/3)−1= ((∣p∣)/3) the question is wrong
$$\underset{{u}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{8}−\mathrm{4}{u}+{u}^{\mathrm{3}} }\:−\:\sqrt[{\mathrm{3}\:}]{\mathrm{8}+\mid{p}\mid\:{u}−{u}^{\mathrm{3}} }}{{u}} \\ $$$$=\:\underset{{u}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\frac{\frac{\mathrm{3}{u}^{\mathrm{2}} −\mathrm{4}}{\mathrm{3}\left(\sqrt[{\mathrm{3}\:}]{\left(\mathrm{8}−\mathrm{4}{u}+{u}^{\mathrm{3}} \right)^{\mathrm{2}} }\right.}−\:\frac{\left(−\mathrm{3}{u}^{\mathrm{2}} +\mid{p}\mid\right)}{\mathrm{3}\left(\sqrt[{\mathrm{3}\:}]{\left(\mathrm{8}+\mid{p}\mid{u}−{u}^{\mathrm{3}} \right)^{\mathrm{2}} }\right.}}{\mathrm{1}} \\ $$$$=\:\frac{−\mathrm{4}}{\mathrm{3}.\mathrm{4}}−\frac{\mid{p}\mid}{\mathrm{3}.\mathrm{4}}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:−\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}=\:\frac{\mid{p}\mid}{\mathrm{3}} \\ $$$${the}\:{question}\:{is}\:{wrong}\: \\ $$
Commented by mathmax by abdo last updated on 19/Feb/20
we have^3 (√(8x^3 −4x^2 +1))=^3 (√(8x^3 (1−(1/(2x))+(1/(8x^3 ))))) =2x(√(1−(1/(2x))+(1/(8x^3 )))) ∼ 2x(1+(1/2)(−(1/(2x)) +(1/(8x^3 )))) (x→−∞) =2x{1−(1/(4x)) +(1/(16x^3 ))} =2x−(1/2) +(1/(8x^2 )) also we have^3 (√(8x^3 +∣p∣x^2 −1))=^3 (√(8x^3 (1+((∣p∣)/(8x))−(1/(8x^3 ))))) =2x(√(1+((∣p∣)/(8x))−(1/(8x^3 ))))∼2x{1+(1/2)(((∣p∣)/(8x))−(1/(8x^3 )))} =2x{1+((∣p∣)/(16x))−(1/(16x^3 ))} =2x +((∣p∣)/8)−(1/(8x^2 )) ⇒ (...)−(....)∼2x−(1/2) +(1/(8x^2 ))−2x−((∣p∣)/8) +(1/(8x^2 )) ∼−(1/2)−((∣p∣)/8) ⇒ lim_(x→−∞) (....)=−(1/2)−((∣p∣)/8) =(1/4) ⇒−((∣p∣)/8) =(1/2)+(1/4) =(3/4) impossible with absolute value so there is a error in the Q.
$${we}\:{have}\:^{\mathrm{3}} \sqrt{\mathrm{8}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{1}}=^{\mathrm{3}} \sqrt{\mathrm{8}{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }\right)} \\ $$$$=\mathrm{2}{x}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }}\:\sim\:\mathrm{2}{x}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{2}{x}}\:+\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }\right)\right)\:\left({x}\rightarrow−\infty\right) \\ $$$$=\mathrm{2}{x}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}{x}}\:+\frac{\mathrm{1}}{\mathrm{16}{x}^{\mathrm{3}} }\right\}\:=\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{2}} }\:\:{also} \\ $$$$\:{we}\:{have}\:^{\mathrm{3}} \sqrt{\mathrm{8}{x}^{\mathrm{3}} +\mid{p}\mid{x}^{\mathrm{2}} −\mathrm{1}}=^{\mathrm{3}} \sqrt{\mathrm{8}{x}^{\mathrm{3}} \left(\mathrm{1}+\frac{\mid{p}\mid}{\mathrm{8}{x}}−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }\right)} \\ $$$$=\mathrm{2}{x}\sqrt{\mathrm{1}+\frac{\mid{p}\mid}{\mathrm{8}{x}}−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }}\sim\mathrm{2}{x}\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mid{p}\mid}{\mathrm{8}{x}}−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }\right)\right\} \\ $$$$=\mathrm{2}{x}\left\{\mathrm{1}+\frac{\mid{p}\mid}{\mathrm{16}{x}}−\frac{\mathrm{1}}{\mathrm{16}{x}^{\mathrm{3}} }\right\}\:=\mathrm{2}{x}\:+\frac{\mid{p}\mid}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\left(…\right)−\left(….\right)\sim\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{2}} }−\mathrm{2}{x}−\frac{\mid{p}\mid}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{2}} }\:\sim−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mid{p}\mid}{\mathrm{8}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow−\infty} \left(….\right)=−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mid{p}\mid}{\mathrm{8}}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow−\frac{\mid{p}\mid}{\mathrm{8}}\:=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\:=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${impossible}\:{with}\:{absolute}\:{value}\:{so}\:{there}\:{is}\:{a}\:{error}\:{in}\:{the}\:{Q}. \\ $$
Commented by mathmax by abdo last updated on 19/Feb/20
sorry error at line 4 we have ^3 (√(8x^3 +∣px∣^2 −1 ))=^3 (√(8x^3 +p^2 x^2 −1))=^3 (√(8x^3 (1+(p^2 /(8x))−(1/(8x^3 ))))) =2x(√(1+(p^2 /(8x))−(1/(8x^3 ))))∼2x{1+(1/2)((p^2 /(8x))−(1/(8x^3 )))} =2x+x((p^2 /(8x))−(1/(8x^3 ))) =2x+(p^2 /8)−(1/(8x^3 )) but the error still existing...
$${sorry}\:{error}\:{at}\:{line}\:\mathrm{4}\:{we}\:{have} \\ $$$$\left.\:\:^{\mathrm{3}} \sqrt{\mathrm{8}{x}^{\mathrm{3}} +\mid{px}\mid^{\mathrm{2}} −\mathrm{1}\:}=^{\mathrm{3}} \sqrt{\mathrm{8}{x}^{\mathrm{3}} \:+{p}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{1}}=^{\mathrm{3}} \sqrt{\mathrm{8}{x}^{\mathrm{3}} \left(\mathrm{1}+\frac{{p}^{\mathrm{2}} }{\mathrm{8}{x}}−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }\right.}\right) \\ $$$$=\mathrm{2}{x}\sqrt{\mathrm{1}+\frac{{p}^{\mathrm{2}} }{\mathrm{8}{x}}−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }}\sim\mathrm{2}{x}\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{p}^{\mathrm{2}} }{\mathrm{8}{x}}−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }\right)\right\} \\ $$$$=\mathrm{2}{x}+{x}\left(\frac{{p}^{\mathrm{2}} }{\mathrm{8}{x}}−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }\right)\:=\mathrm{2}{x}+\frac{{p}^{\mathrm{2}} }{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}{x}^{\mathrm{3}} }\:\:\:{but}\:{the}\:{error}\:{still}\:{existing}… \\ $$
Answered by mr W last updated on 20/Feb/20
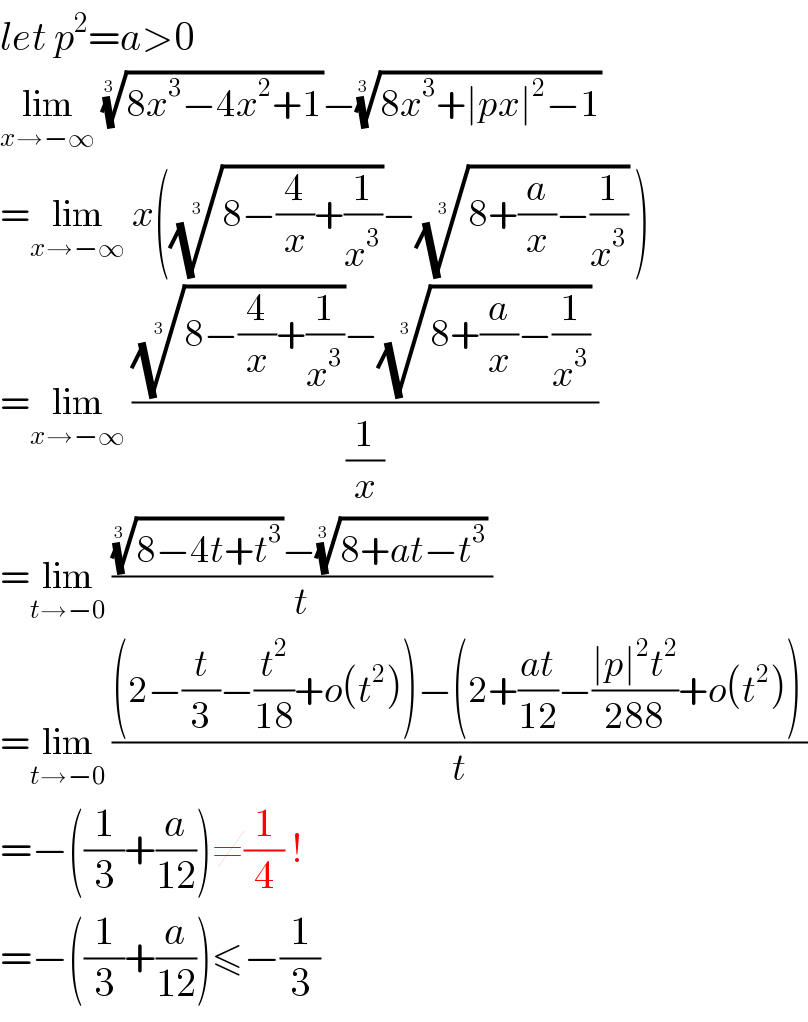
let p^2 =a>0 lim_(x→−∞) ((8x^3 −4x^2 +1))^(1/(3 )) −((8x^3 +∣px∣^2 −1))^(1/(3 )) =lim_(x→−∞) x(((8−(4/x)+(1/x^3 )))^(1/(3 )) −((8+(a/x)−(1/x^3 )))^(1/(3 )) ) =lim_(x→−∞) ((((8−(4/x)+(1/x^3 )))^(1/(3 )) −((8+(a/x)−(1/x^3 )))^(1/(3 )) )/(1/x)) =lim_(t→−0) ((((8−4t+t^3 ))^(1/(3 )) −((8+at−t^3 ))^(1/(3 )) )/t) =lim_(t→−0) (((2−(t/3)−(t^2 /(18))+o(t^2 ))−(2+((at)/(12))−((∣p∣^2 t^2 )/(288))+o(t^2 )) )/t) =−((1/3)+(a/(12)))≠(1/4) ! =−((1/3)+(a/(12)))≤−(1/3)
$${let}\:{p}^{\mathrm{2}} ={a}>\mathrm{0} \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{3}\:}]{\mathrm{8}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}}−\sqrt[{\mathrm{3}\:}]{\mathrm{8}{x}^{\mathrm{3}} +\mid{px}\mid^{\mathrm{2}} −\mathrm{1}}\: \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{x}\left(\sqrt[{\mathrm{3}\:}]{\mathrm{8}−\frac{\mathrm{4}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}−\sqrt[{\mathrm{3}\:}]{\mathrm{8}+\frac{{a}}{{x}}−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}\:\right) \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{8}−\frac{\mathrm{4}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}−\sqrt[{\mathrm{3}\:}]{\mathrm{8}+\frac{{a}}{{x}}−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}\:}{\frac{\mathrm{1}}{{x}}} \\ $$$$=\underset{{t}\rightarrow−\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{8}−\mathrm{4}{t}+{t}^{\mathrm{3}} }−\sqrt[{\mathrm{3}\:}]{\mathrm{8}+{at}−{t}^{\mathrm{3}} }\:}{{t}} \\ $$$$=\underset{{t}\rightarrow−\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{2}−\frac{{t}}{\mathrm{3}}−\frac{{t}^{\mathrm{2}} }{\mathrm{18}}+{o}\left({t}^{\mathrm{2}} \right)\right)−\left(\mathrm{2}+\frac{{at}}{\mathrm{12}}−\frac{\mid{p}\mid^{\mathrm{2}} {t}^{\mathrm{2}} }{\mathrm{288}}+{o}\left({t}^{\mathrm{2}} \right)\right)\:}{{t}} \\ $$$$=−\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{{a}}{\mathrm{12}}\right)\neq\frac{\mathrm{1}}{\mathrm{4}}\:! \\ $$$$=−\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{{a}}{\mathrm{12}}\right)\leqslant−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by jagoll last updated on 19/Feb/20
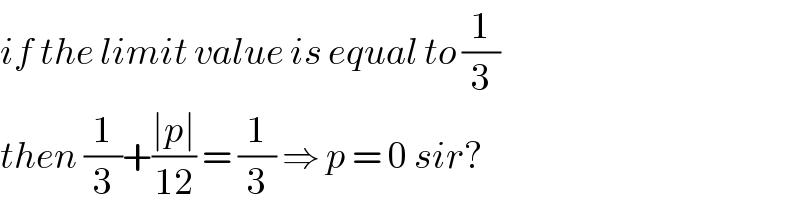
if the limit value is equal to (1/3) then (1/3)+((∣p∣)/(12)) = (1/3) ⇒ p = 0 sir?
$${if}\:{the}\:{limit}\:{value}\:{is}\:{equal}\:{to}\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${then}\:\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mid{p}\mid}{\mathrm{12}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:{p}\:=\:\mathrm{0}\:{sir}? \\ $$
Commented by mr W last updated on 19/Feb/20
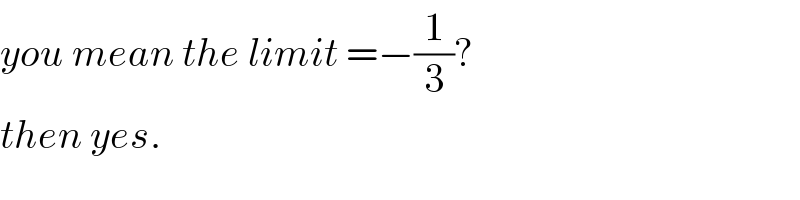
you mean the limit =−(1/3)? then yes.
$${you}\:{mean}\:{the}\:{limit}\:=−\frac{\mathrm{1}}{\mathrm{3}}?\: \\ $$$${then}\:{yes}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *