lim-x-a-1-b-1-x-a-x-a-b-gt-0-

Question Number 34554 by rahul 19 last updated on 07/May/18

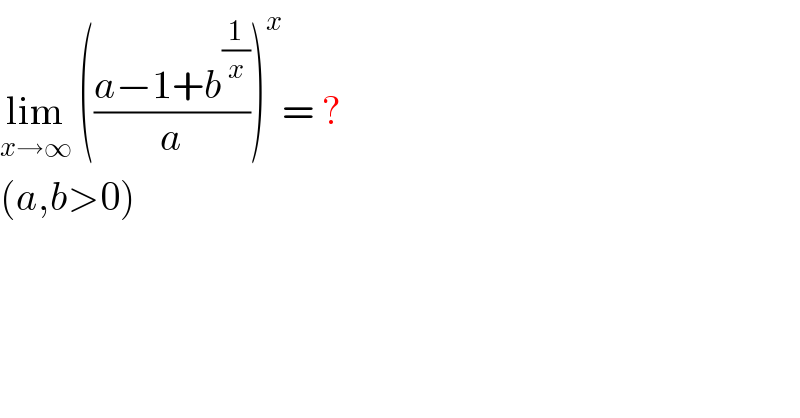
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{a}−\mathrm{1}+{b}^{\frac{\mathrm{1}}{{x}}} }{{a}}\right)^{{x}} =\:? \\ $$$$\left({a},{b}>\mathrm{0}\right) \\ $$

Commented by math khazana by abdo last updated on 09/May/18

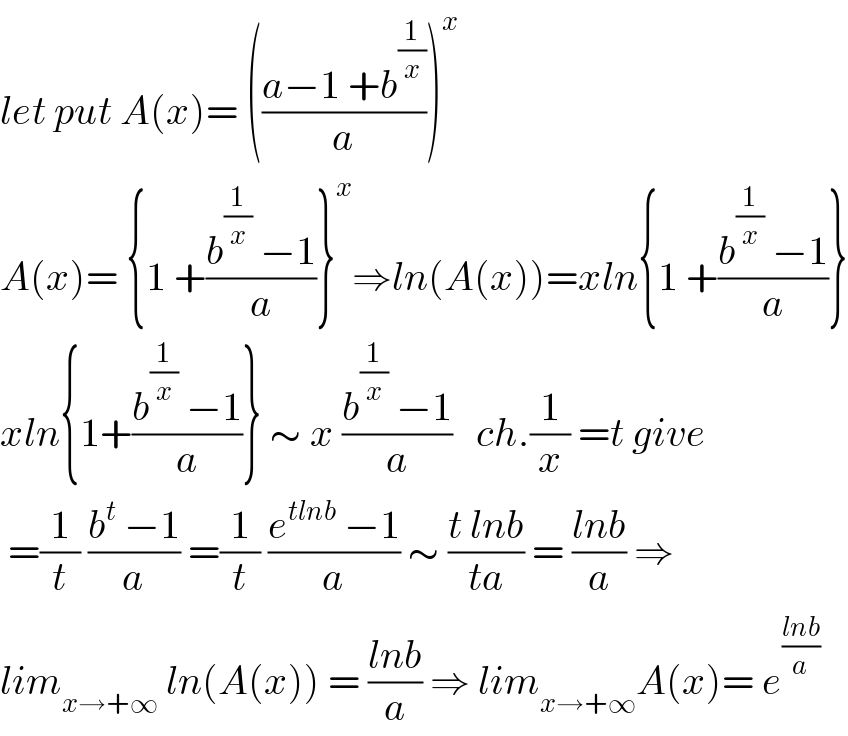
$${let}\:{put}\:{A}\left({x}\right)=\:\left(\frac{{a}−\mathrm{1}\:+{b}^{\frac{\mathrm{1}}{{x}}} }{{a}}\right)^{{x}} \\ $$$${A}\left({x}\right)=\:\left\{\mathrm{1}\:+\frac{{b}^{\frac{\mathrm{1}}{{x}}} \:−\mathrm{1}}{{a}}\right\}^{{x}} \Rightarrow{ln}\left({A}\left({x}\right)\right)={xln}\left\{\mathrm{1}\:+\frac{{b}^{\frac{\mathrm{1}}{{x}}} \:−\mathrm{1}}{{a}}\right\} \\ $$$${xln}\left\{\mathrm{1}+\frac{{b}^{\frac{\mathrm{1}}{{x}}} \:−\mathrm{1}}{{a}}\right\}\:\sim\:{x}\:\frac{{b}^{\frac{\mathrm{1}}{{x}}} \:−\mathrm{1}}{{a}}\:\:\:{ch}.\frac{\mathrm{1}}{{x}}\:={t}\:{give} \\ $$$$\:=\frac{\mathrm{1}}{{t}}\:\frac{{b}^{{t}} \:−\mathrm{1}}{{a}}\:=\frac{\mathrm{1}}{{t}}\:\frac{{e}^{{tlnb}} \:−\mathrm{1}}{{a}}\:\sim\:\frac{{t}\:{lnb}}{{ta}}\:=\:\frac{{lnb}}{{a}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} \:{ln}\left({A}\left({x}\right)\right)\:=\:\frac{{lnb}}{{a}}\:\Rightarrow\:{lim}_{{x}\rightarrow+\infty} {A}\left({x}\right)=\:{e}^{\frac{{lnb}}{{a}}} \\ $$

Commented by Joel578 last updated on 10/May/18

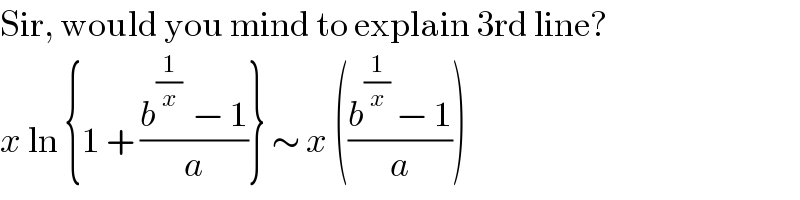
$$\mathrm{Sir},\:\mathrm{would}\:\mathrm{you}\:\mathrm{mind}\:\mathrm{to}\:\mathrm{explain}\:\mathrm{3rd}\:\mathrm{line}? \\ $$$${x}\:\mathrm{ln}\:\left\{\mathrm{1}\:+\:\frac{{b}^{\frac{\mathrm{1}}{{x}}\:} \:−\:\mathrm{1}}{{a}}\right\}\:\sim\:{x}\:\left(\frac{{b}^{\frac{\mathrm{1}}{{x}}} \:−\:\mathrm{1}}{{a}}\right) \\ $$

Commented by abdo mathsup 649 cc last updated on 11/May/18

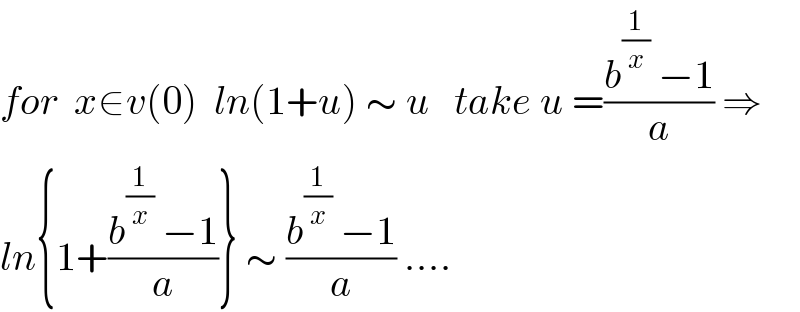
$${for}\:\:{x}\in{v}\left(\mathrm{0}\right)\:\:{ln}\left(\mathrm{1}+{u}\right)\:\sim\:{u}\:\:\:{take}\:{u}\:=\frac{{b}^{\frac{\mathrm{1}}{{x}}} \:−\mathrm{1}}{{a}}\:\Rightarrow \\ $$$${ln}\left\{\mathrm{1}+\frac{{b}^{\frac{\mathrm{1}}{{x}}} \:−\mathrm{1}}{{a}}\right\}\:\sim\:\frac{{b}^{\frac{\mathrm{1}}{{x}}} \:−\mathrm{1}}{{a}}\:…. \\ $$

Answered by Joel578 last updated on 08/May/18

$$\:\:\:\:\:{L}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{a}\:+\:{b}^{\frac{\mathrm{1}}{{x}}} \:−\:\mathrm{1}}{{a}}\right)^{{x}} \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[{x}\:.\:\mathrm{ln}\:\left(\frac{{a}\:+\:{b}^{\frac{\mathrm{1}}{{x}}} \:−\:\mathrm{1}}{{a}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\frac{\mathrm{ln}\:\left(\frac{{a}\:+\:{b}^{\mathrm{1}/{x}} \:−\:\mathrm{1}}{{a}}\right)}{\mathrm{1}/{x}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\frac{−\frac{\mathrm{ln}\:{b}\:.\:{b}^{\mathrm{1}/{x}} }{{x}^{\mathrm{2}} \left({a}\:+\:{b}^{\mathrm{1}/{x}} \:−\:\mathrm{1}\right)}}{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\frac{\mathrm{ln}\:{b}\:.\:{b}^{\mathrm{1}/{x}} }{{a}\:+\:{b}^{\mathrm{1}/{x}} \:−\:\mathrm{1}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\mathrm{ln}\:{b}\left[\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{b}^{\mathrm{1}/{x}} }{{a}\:+\:{b}^{\mathrm{1}/{x}} \:−\:\mathrm{1}}\right)\right]\:=\:\mathrm{ln}\:{b}\:.\:\left(\frac{\mathrm{1}}{{a}\:+\:\mathrm{1}\:−\:\mathrm{1}}\right) \\ $$$$\mathrm{ln}\:{L}\:=\:\left(\frac{\mathrm{1}}{{a}}\right)\:.\:\mathrm{ln}\:{b}\:=\:\mathrm{ln}\:\left({b}^{\frac{\mathrm{1}}{{a}}} \right) \\ $$$${L}\:=\:{b}^{\frac{\mathrm{1}}{{a}}} \\ $$

Commented by rahul 19 last updated on 12/May/18

$${Sir}\:,\:{pls}\:{explain}\:{numerator}\:{of}\:{line}\:\mathrm{3}\:\left({i}\:{know}\:{you}\right. \\ $$$$\left.{have}\:{use}\:{l}−{hospital}.\right) \\ $$

Commented by rahul 19 last updated on 12/May/18

��

Terms of Service
Privacy Policy
Contact: info@tinkutara.com