Question Number 107882 by Ar Brandon last updated on 13/Aug/20
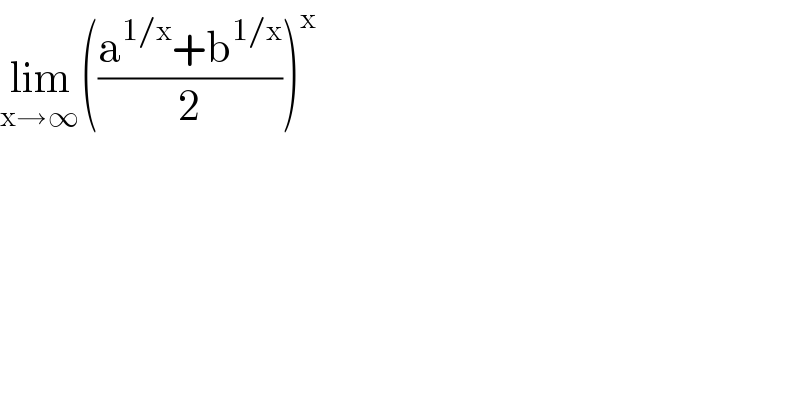
$$\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{a}^{\mathrm{1}/\mathrm{x}} +\mathrm{b}^{\mathrm{1}/\mathrm{x}} }{\mathrm{2}}\right)^{\mathrm{x}} \\ $$
Commented by bemath last updated on 13/Aug/20

$${coolll} \\ $$
Commented by bemath last updated on 13/Aug/20
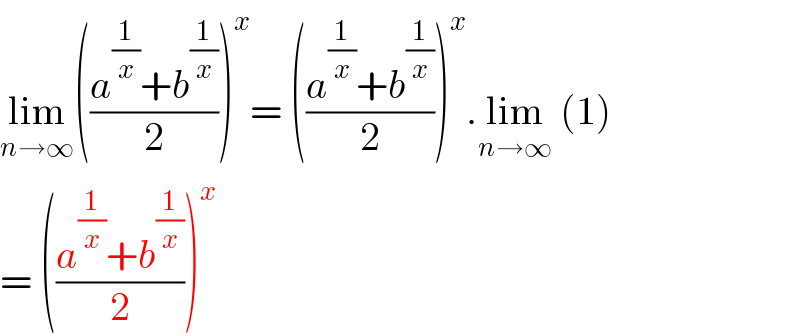
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{a}^{\frac{\mathrm{1}}{{x}}} +{b}^{\frac{\mathrm{1}}{{x}}} }{\mathrm{2}}\right)^{{x}} =\:\left(\frac{{a}^{\frac{\mathrm{1}}{{x}}} +{b}^{\frac{\mathrm{1}}{{x}}} }{\mathrm{2}}\right)^{{x}} .\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\right) \\ $$$$=\:\left(\frac{{a}^{\frac{\mathrm{1}}{{x}}} +{b}^{\frac{\mathrm{1}}{{x}}} }{\mathrm{2}}\right)^{{x}} \\ $$
Commented by Ar Brandon last updated on 13/Aug/20
�� Sorry I meant x instead of n
Commented by bemath last updated on 13/Aug/20
��������
Commented by kaivan.ahmadi last updated on 13/Aug/20

$${lim}_{{x}\rightarrow\infty} \left(\frac{{a}^{\frac{\mathrm{1}}{{x}}} +{b}^{\frac{\mathrm{1}}{{x}}} }{\mathrm{2}}−\mathrm{1}\right)\left({x}\right)={lim}_{{x}\rightarrow\infty} \left(\frac{{a}^{\frac{\mathrm{1}}{{x}}} +{b}^{\frac{\mathrm{1}}{{x}}} −\mathrm{2}}{\mathrm{2}}\right)\left({x}\right) \\ $$$$={lim}_{{x}\rightarrow\infty} \frac{{a}^{\frac{\mathrm{1}}{{x}}} +{b}^{\frac{\mathrm{1}}{{x}}} −\mathrm{2}}{\frac{\mathrm{2}}{{x}}}\:\:\overset{{Hop}} {=}\:\:{lim}_{{x}\rightarrow\infty} \frac{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{a}^{\frac{\mathrm{1}}{{x}}} {lna}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{b}^{\frac{\mathrm{1}}{{x}}} {lnb}}{\frac{−\mathrm{2}}{{x}^{\mathrm{2}} }}= \\ $$$${lim}_{{x}\rightarrow\infty} \frac{{a}^{\frac{\mathrm{1}}{{x}}} {lna}+{b}^{\frac{\mathrm{1}}{{x}}} {lnb}}{\mathrm{2}}=\frac{{lna}+{lnb}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by pticantor last updated on 14/Aug/20

$$ \\ $$$$\sqrt{{ab}} \\ $$
