Question Number 115541 by bobhans last updated on 26/Sep/20
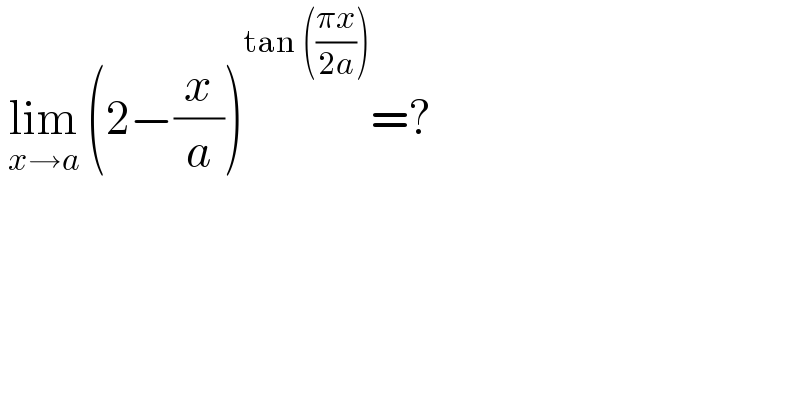
$$\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\left(\mathrm{2}−\frac{{x}}{{a}}\right)^{\mathrm{tan}\:\left(\frac{\pi{x}}{\mathrm{2}{a}}\right)} =? \\ $$
Answered by bemath last updated on 26/Sep/20

$${L}\:=\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\left(\mathrm{2}−\frac{{x}}{{a}}\right)^{\mathrm{tan}\:\left(\frac{\pi{x}}{\mathrm{2}{a}}\right)} \\ $$$$\mathrm{ln}\:{L}=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{2}−\frac{{x}}{{a}}\right)}{\mathrm{cot}\:\left(\frac{\pi{x}}{\mathrm{2}{a}}\right)} \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{−\frac{\mathrm{1}}{{a}}}{\mathrm{2}−\frac{{x}}{{a}}}\:.\:\frac{\mathrm{1}}{\left(−\frac{\pi}{\mathrm{2}{a}}\:\mathrm{csc}^{\mathrm{2}} \left(\frac{\pi{x}}{{a}}\right)\right)} \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{\mathrm{2}.\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi{x}}{\mathrm{2}{a}}\right)}{\pi\:\left(\frac{\mathrm{2}{a}−{x}}{{a}}\right)}\:=\:\frac{\mathrm{2}}{\pi} \\ $$$${L}\:=\:{e}^{\frac{\mathrm{2}}{\pi}} \:=\:\sqrt[{\pi\:}]{{e}^{\mathrm{2}} } \\ $$
Answered by Dwaipayan Shikari last updated on 26/Sep/20

$$\underset{{x}\rightarrow\mathrm{a}} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{1}−\frac{\mathrm{x}}{\mathrm{a}}\right)^{\mathrm{tan}\left(\frac{\pi\mathrm{x}}{\mathrm{2a}}\right)} =\mathrm{y} \\ $$$$\underset{{x}\rightarrow\mathrm{a}} {\mathrm{lim}tan}\left(\frac{\pi\mathrm{x}}{\mathrm{2a}}\right)\mathrm{log}\left(\mathrm{1}+\mathrm{1}−\frac{\mathrm{x}}{\mathrm{a}}\right)=\mathrm{logy} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{a}}\right)\mathrm{tan}\left(\frac{\pi\mathrm{x}}{\mathrm{2a}}\right)=\mathrm{logy} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{a}}\right)\mathrm{sin}\left(\frac{\pi\mathrm{x}}{\mathrm{2a}}\right).\frac{\mathrm{1}}{\mathrm{cos}\left(\frac{\pi\mathrm{x}}{\mathrm{2a}}\right)}=\mathrm{logy} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{a}}\right)\frac{\mathrm{1}}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi\mathrm{x}}{\mathrm{2a}}\right)}=\mathrm{logy} \\ $$$$\frac{\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{a}}\right)}{\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{a}}\right)}=\mathrm{logy} \\ $$$$\mathrm{y}=\mathrm{e}^{\frac{\mathrm{2}}{\pi}} \\ $$$$ \\ $$
Answered by mnjuly1970 last updated on 26/Sep/20
![solution: 1−(x/a) =t {_(t→0) ^(x→a) lim_(t→0) (1+t)^(tan[(π/2)(1−t)]) =lim_(t→0 ) (1+t)^(cot((π/2)t)) =_(t→0) ^( sin((π/2)t)∽(π/2)t) lim_(t→0) [((1+t)^(2/π) )^(1/t) ]^(cos((π/2)t)) =_(t→0) ^(cos((π/2)t)→1) =e^(2/π) ✓ m.n.july.1970](https://www.tinkutara.com/question/Q115553.png)
$$\:{solution}:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}−\frac{{x}}{{a}}\:={t}\:\left\{_{{t}\rightarrow\mathrm{0}} ^{{x}\rightarrow{a}} \right. \\ $$$$\:\:{lim}_{{t}\rightarrow\mathrm{0}} \:\left(\mathrm{1}+{t}\right)^{{tan}\left[\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−{t}\right)\right]} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}\:} \left(\mathrm{1}+{t}\right)^{{cot}\left(\frac{\pi}{\mathrm{2}}{t}\right)} \underset{{t}\rightarrow\mathrm{0}} {\overset{\:\:\:\:\:\:{sin}\left(\frac{\pi}{\mathrm{2}}{t}\right)\backsim\frac{\pi}{\mathrm{2}}{t}} {=}} \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} \left[\left(\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{2}}{\pi}} \right)^{\frac{\mathrm{1}}{{t}}} \right]^{{cos}\left(\frac{\pi}{\mathrm{2}}{t}\right)} \underset{{t}\rightarrow\mathrm{0}} {\overset{{cos}\left(\frac{\pi}{\mathrm{2}}{t}\right)\rightarrow\mathrm{1}} {=}} \\ $$$$\:\:\:\:\:={e}^{\frac{\mathrm{2}}{\pi}} \:\checkmark \\ $$$$\:\:\:\:\:\:\:{m}.{n}.{july}.\mathrm{1970} \\ $$
