Question Number 149239 by john_santu last updated on 04/Aug/21
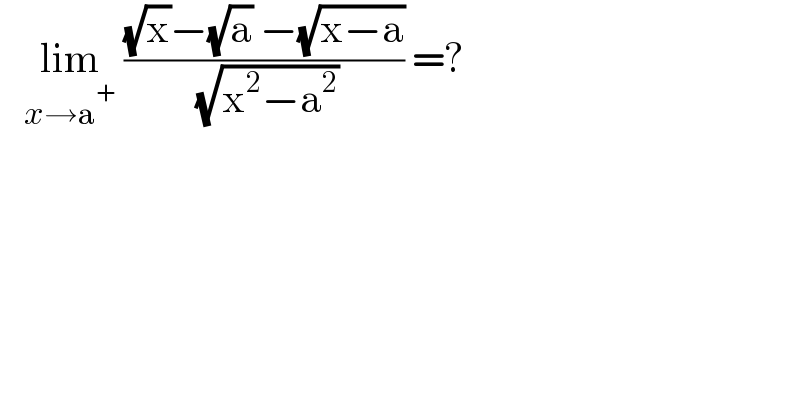
$$\:\:\:\underset{{x}\rightarrow\mathrm{a}^{+} } {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}}−\sqrt{\mathrm{a}}\:−\sqrt{\mathrm{x}−\mathrm{a}}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }}\:=?\: \\ $$
Answered by EDWIN88 last updated on 04/Aug/21
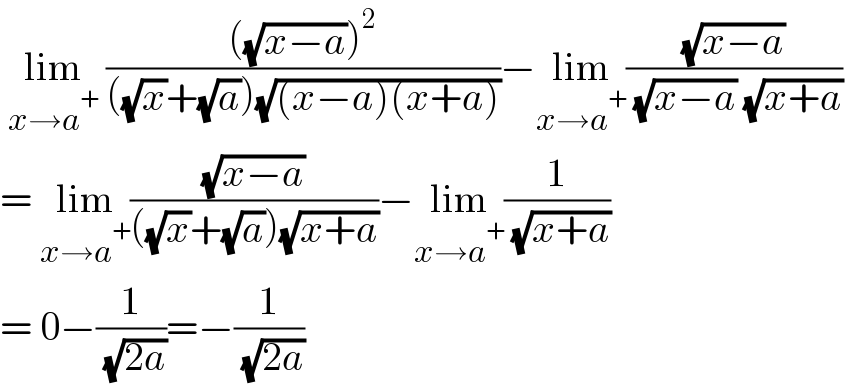
$$\:\underset{{x}\rightarrow{a}^{+} } {\mathrm{lim}}\:\frac{\left(\sqrt{{x}−{a}}\right)^{\mathrm{2}} }{\left(\sqrt{{x}}+\sqrt{{a}}\right)\sqrt{\left({x}−{a}\right)\left({x}+{a}\right)}}−\underset{{x}\rightarrow{a}^{+} } {\mathrm{lim}}\frac{\sqrt{{x}−{a}}}{\:\sqrt{{x}−{a}}\:\sqrt{{x}+{a}}} \\ $$$$=\:\underset{{x}\rightarrow{a}^{+} } {\mathrm{lim}}\frac{\sqrt{{x}−{a}}}{\left(\sqrt{{x}}+\sqrt{{a}}\right)\sqrt{{x}+{a}}}−\underset{{x}\rightarrow{a}^{+} } {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{{x}+{a}}} \\ $$$$=\:\mathrm{0}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}\: \\ $$
