Question Number 121638 by bemath last updated on 10/Nov/20
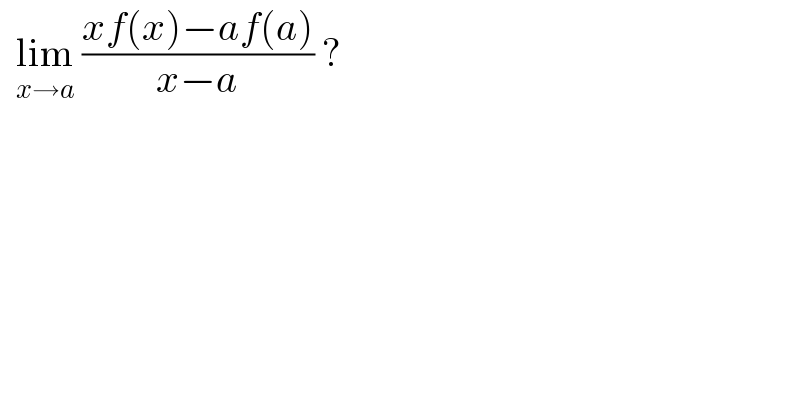
$$\:\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{xf}\left({x}\right)−{af}\left({a}\right)}{{x}−{a}}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 10/Nov/20
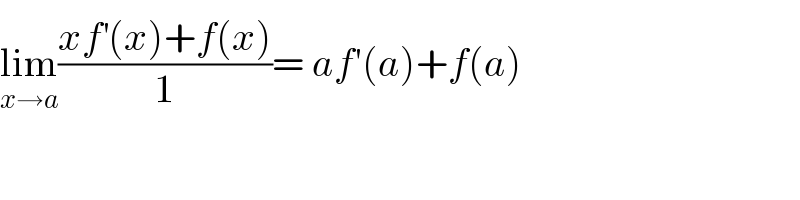
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{xf}^{'} \left({x}\right)+{f}\left({x}\right)}{\mathrm{1}}=\:{af}'\left({a}\right)+{f}\left({a}\right) \\ $$
Answered by TANMAY PANACEA last updated on 10/Nov/20
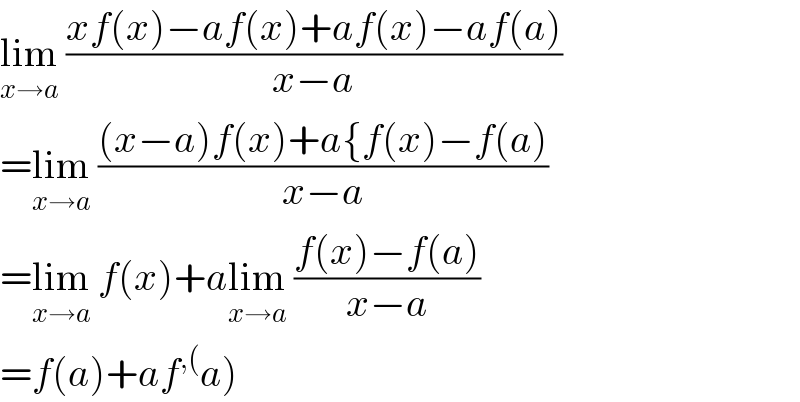
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{xf}\left({x}\right)−{af}\left({x}\right)+{af}\left({x}\right)−{af}\left({a}\right)}{{x}−{a}} \\ $$$$=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{\left({x}−{a}\right){f}\left({x}\right)+{a}\left\{{f}\left({x}\right)−{f}\left({a}\right)\right.}{{x}−{a}} \\ $$$$=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:{f}\left({x}\right)+{a}\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{f}\left({x}\right)−{f}\left({a}\right)}{{x}−{a}} \\ $$$$\left.={f}\left({a}\right)+{af}^{,\left(\right.} {a}\right) \\ $$
