Menu Close

lim-x-cos-4-x-1-3-1-cos-2-x-cos-4-x-

Tinku Tara 0 Comments
Pin




Question Number 114239 by bemath last updated on 18/Sep/20
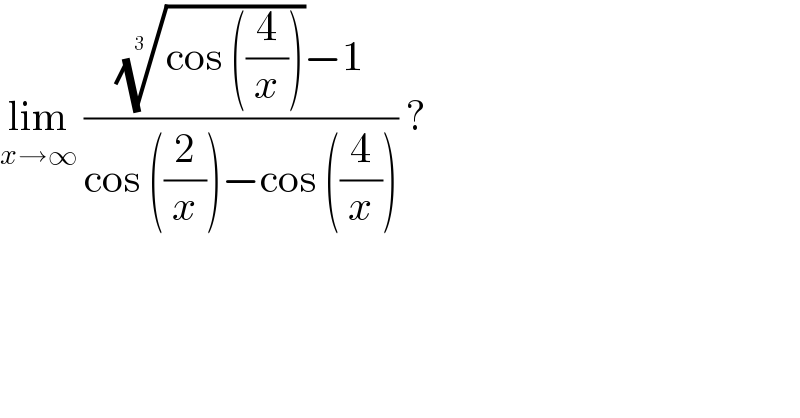
lim_(x→∞) ((((cos ((4/x))))^(1/(3 )) −1)/(cos ((2/x))−cos ((4/x)))) ?
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{cos}\:\left(\frac{\mathrm{4}}{{x}}\right)}−\mathrm{1}}{\mathrm{cos}\:\left(\frac{\mathrm{2}}{{x}}\right)−\mathrm{cos}\:\left(\frac{\mathrm{4}}{{x}}\right)}\:? \\ $$
Commented by bemath last updated on 18/Sep/20
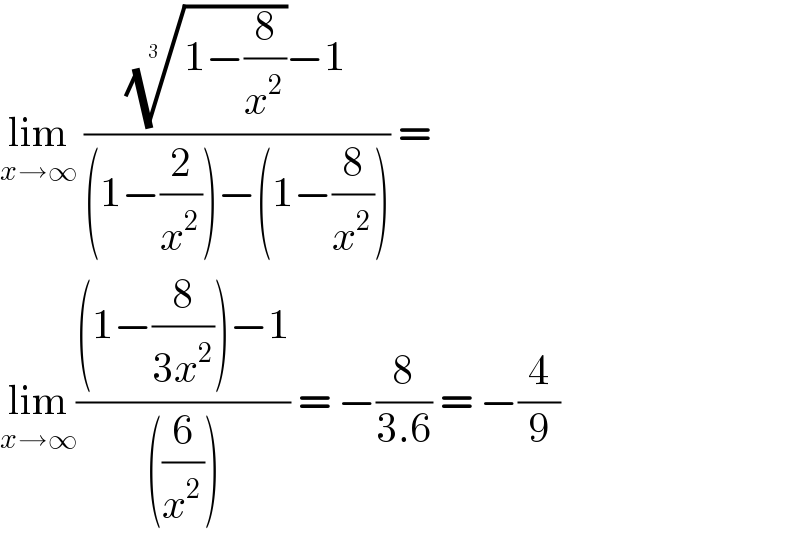
lim_(x→∞) ((((1−(8/x^2 )))^(1/(3 )) −1)/((1−(2/x^2 ))−(1−(8/x^2 )))) = lim_(x→∞) (((1−(8/(3x^2 )))−1)/(((6/x^2 )))) = −(8/(3.6)) = −(4/9)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{1}−\frac{\mathrm{8}}{{x}^{\mathrm{2}} }}−\mathrm{1}}{\left(\mathrm{1}−\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\mathrm{8}}{{x}^{\mathrm{2}} }\right)}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{1}−\frac{\mathrm{8}}{\mathrm{3}{x}^{\mathrm{2}} }\right)−\mathrm{1}}{\left(\frac{\mathrm{6}}{{x}^{\mathrm{2}} }\right)}\:=\:−\frac{\mathrm{8}}{\mathrm{3}.\mathrm{6}}\:=\:−\frac{\mathrm{4}}{\mathrm{9}} \\ $$
Answered by Dwaipayan Shikari last updated on 18/Sep/20
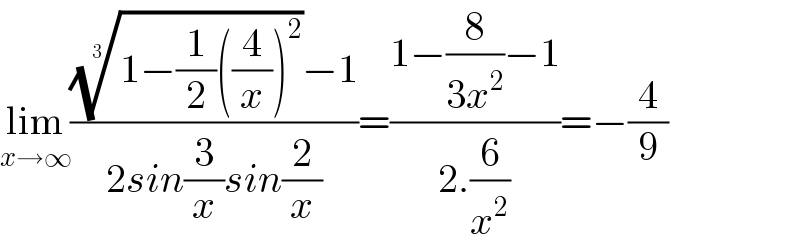
lim_(x→∞) ((((1−(1/2)((4/x))^2 ))^(1/3) −1)/(2sin(3/x)sin(2/x)))=((1−(8/(3x^2 ))−1)/(2.(6/x^2 )))=−(4/9)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}}{{x}}\right)^{\mathrm{2}} }−\mathrm{1}}{\mathrm{2}{sin}\frac{\mathrm{3}}{{x}}{sin}\frac{\mathrm{2}}{{x}}}=\frac{\mathrm{1}−\frac{\mathrm{8}}{\mathrm{3}{x}^{\mathrm{2}} }−\mathrm{1}}{\mathrm{2}.\frac{\mathrm{6}}{{x}^{\mathrm{2}} }}=−\frac{\mathrm{4}}{\mathrm{9}}\: \\ $$
Answered by mathmax by abdo last updated on 19/Sep/20
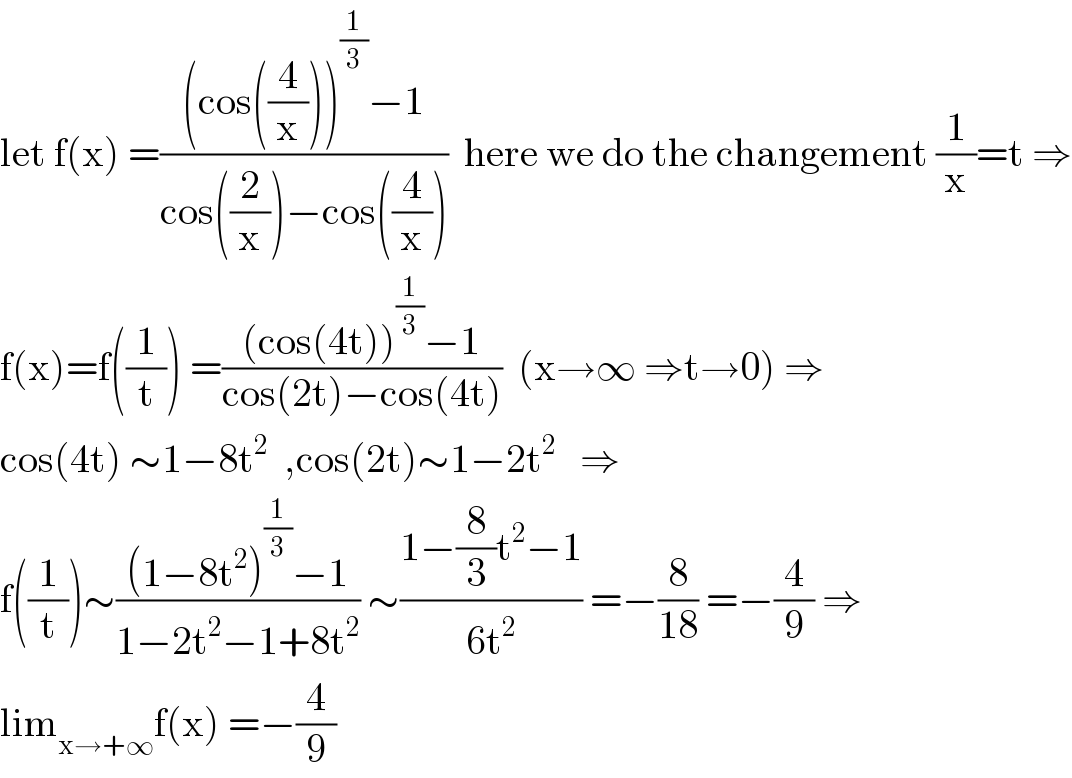
let f(x) =(((cos((4/x)))^(1/3) −1)/(cos((2/x))−cos((4/x)))) here we do the changement (1/x)=t ⇒ f(x)=f((1/t)) =(((cos(4t))^(1/3) −1)/(cos(2t)−cos(4t))) (x→∞ ⇒t→0) ⇒ cos(4t) ∼1−8t^2 ,cos(2t)∼1−2t^2 ⇒ f((1/t))∼(((1−8t^2 )^(1/3) −1)/(1−2t^2 −1+8t^2 )) ∼((1−(8/3)t^2 −1)/(6t^2 )) =−(8/(18)) =−(4/9) ⇒ lim_(x→+∞) f(x) =−(4/9)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\left(\mathrm{cos}\left(\frac{\mathrm{4}}{\mathrm{x}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{1}}{\mathrm{cos}\left(\frac{\mathrm{2}}{\mathrm{x}}\right)−\mathrm{cos}\left(\frac{\mathrm{4}}{\mathrm{x}}\right)}\:\:\mathrm{here}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{t}}\right)\:=\frac{\left(\mathrm{cos}\left(\mathrm{4t}\right)\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{1}}{\mathrm{cos}\left(\mathrm{2t}\right)−\mathrm{cos}\left(\mathrm{4t}\right)}\:\:\left(\mathrm{x}\rightarrow\infty\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{cos}\left(\mathrm{4t}\right)\:\sim\mathrm{1}−\mathrm{8t}^{\mathrm{2}} \:\:,\mathrm{cos}\left(\mathrm{2t}\right)\sim\mathrm{1}−\mathrm{2t}^{\mathrm{2}} \:\:\:\Rightarrow \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{t}}\right)\sim\frac{\left(\mathrm{1}−\mathrm{8t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{1}}{\mathrm{1}−\mathrm{2t}^{\mathrm{2}} −\mathrm{1}+\mathrm{8t}^{\mathrm{2}} }\:\sim\frac{\mathrm{1}−\frac{\mathrm{8}}{\mathrm{3}}\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{6t}^{\mathrm{2}} }\:=−\frac{\mathrm{8}}{\mathrm{18}}\:=−\frac{\mathrm{4}}{\mathrm{9}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=−\frac{\mathrm{4}}{\mathrm{9}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *