lim-x-cos-pi-4-cos-pi-8-cos-pi-2-n-1-

Question Number 174715 by infinityaction last updated on 09/Aug/22

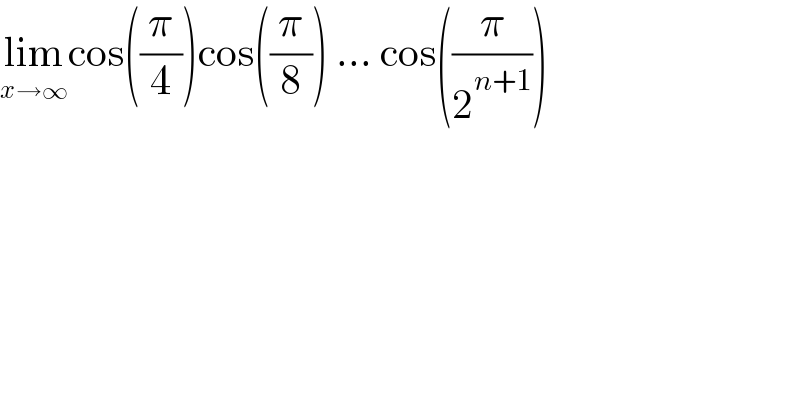
lim_(x→∞) cos((π/4))cos((π/8)) ... cos((π/2^(n+1) ))

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}cos}\left(\frac{\pi}{\mathrm{4}}\right)\mathrm{cos}\left(\frac{\pi}{\mathrm{8}}\right)\:…\:\mathrm{cos}\left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right)\: \\ $$

Answered by abdullahoudou last updated on 09/Aug/22

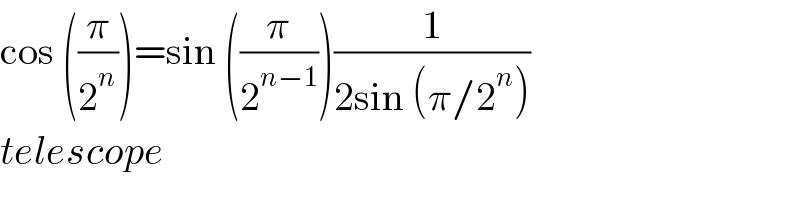
cos ((π/2^n ))=sin ((π/2^(n−1) ))(1/(2sin (π/2^n ))) telescope

$$\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}−\mathrm{1}} }\right)\frac{\mathrm{1}}{\mathrm{2sin}\:\left(\pi/\mathrm{2}^{{n}} \right)} \\ $$$${telescope} \\ $$

Commented by infinityaction last updated on 09/Aug/22

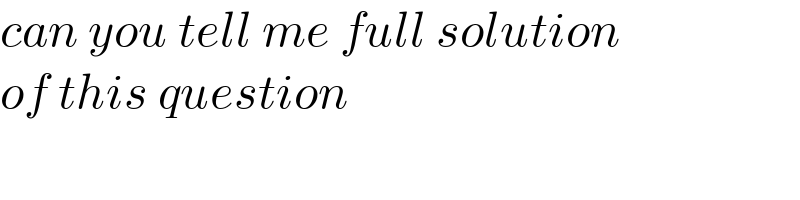
$${can}\:{you}\:{tell}\:{me}\:{full}\:{solution} \\ $$$${of}\:{this}\:{question}\: \\ $$

Answered by princeDera last updated on 10/Aug/22

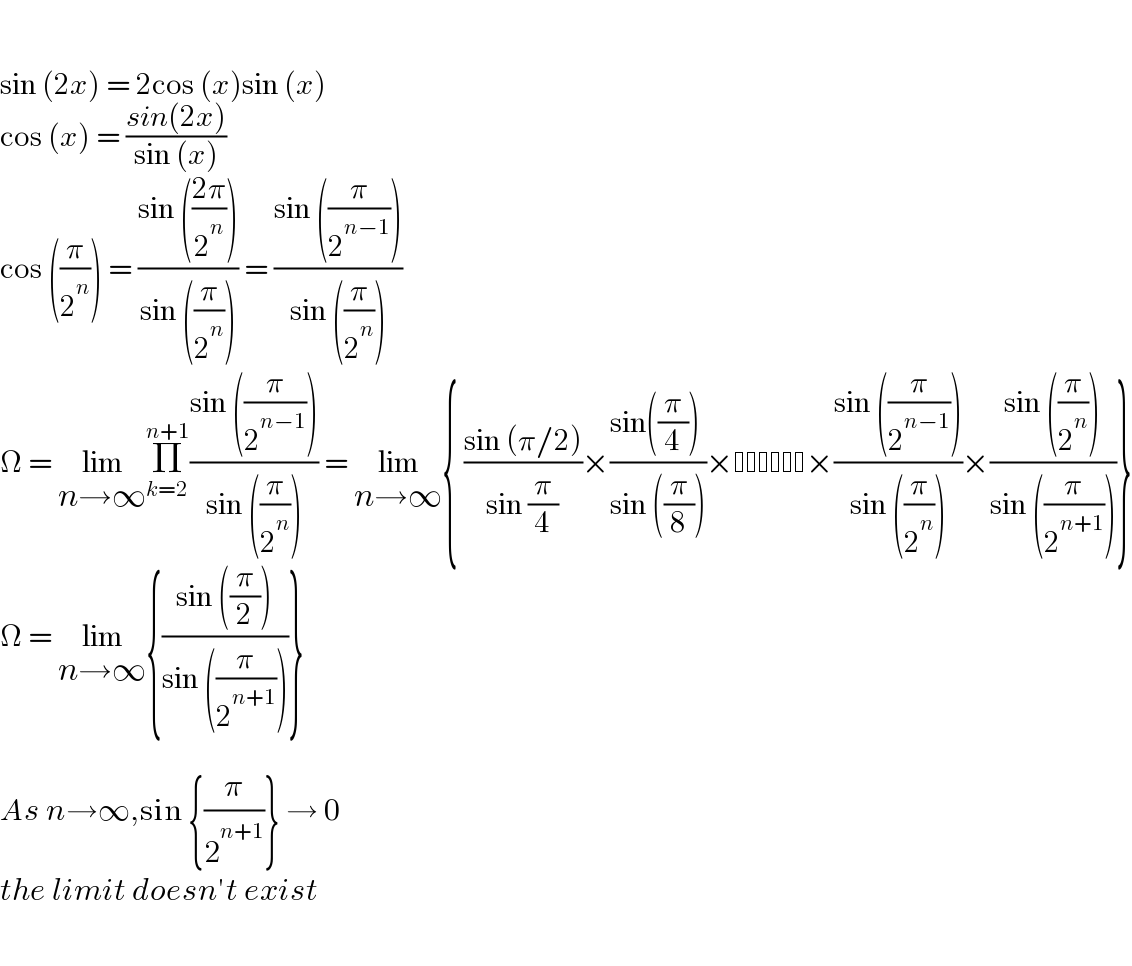
sin (2x) = 2cos (x)sin (x) cos (x) = ((sin(2x))/(sin (x))) cos ((π/2^n )) = ((sin (((2π)/2^n )))/(sin ((π/2^n )))) = ((sin ((π/2^(n−1) )))/(sin ((π/2^n )))) Ω = lim_(n→∞) Π_(k=2) ^(n+1) ((sin ((π/2^(n−1) )))/(sin ((π/2^n )))) = lim_(n→∞) { ((sin (π/2))/(sin (π/4)))×((sin((π/4)) )/(sin ((π/8))))× ×((sin ((π/2^(n−1) )))/(sin ((π/2^n ))))×((sin ((π/2^n )))/(sin ((π/2^(n+1) ))))} Ω = lim_(n→∞) {((sin ((π/2)))/(sin ((π/2^(n+1) ))))} As n→∞,sin {(π/2^(n+1) )} → 0 the limit doesn′t exist

$$ \\ $$$$ \\ $$$$\mathrm{sin}\:\left(\mathrm{2}{x}\right)\:=\:\mathrm{2cos}\:\left({x}\right)\mathrm{sin}\:\left({x}\right) \\ $$$$\mathrm{cos}\:\left({x}\right)\:=\:\frac{{sin}\left(\mathrm{2}{x}\right)}{\mathrm{sin}\:\left({x}\right)} \\ $$$$\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)\:=\:\frac{\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{2}^{{n}} }\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)}\:=\:\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}−\mathrm{1}} }\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)} \\ $$$$\Omega\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\prod}}\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}−\mathrm{1}} }\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\:\frac{\mathrm{sin}\:\left(\pi/\mathrm{2}\right)}{\mathrm{sin}\:\frac{\pi}{\mathrm{4}}}×\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)\:}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{8}}\right)}× ×\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}−\mathrm{1}} }\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)}×\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right)}\right\} \\ $$$$\Omega\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right)}\right\} \\ $$$$ \\ $$$${As}\:{n}\rightarrow\infty,\mathrm{sin}\:\left\{\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right\}\:\rightarrow\:\mathrm{0} \\ $$$${the}\:{limit}\:{doesn}'{t}\:{exist} \\ $$$$ \\ $$

Commented by infinityaction last updated on 09/Aug/22

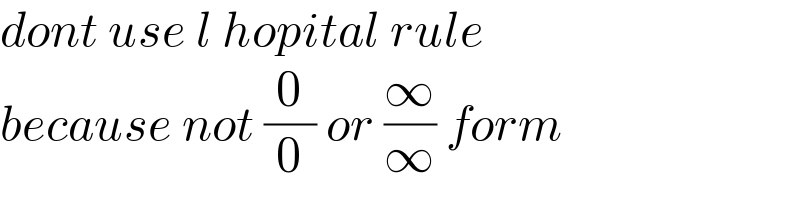
dont use l hopital rule because not (0/0) or (∞/∞) form

$${dont}\:{use}\:{l}\:{hopital}\:{rule} \\ $$$${because}\:{not}\:\frac{\mathrm{0}}{\mathrm{0}}\:{or}\:\frac{\infty}{\infty}\:{form}\: \\ $$

Commented by princeDera last updated on 10/Aug/22

$${yeah} \\ $$$${the}\:{limit}\:{doesn}'{t}\:{exist} \\ $$$$ \\ $$

Facebook Tweet Pin

lim-x-cos-pi-4-cos-pi-8-cos-pi-2-n-1-

Leave a Reply Cancel reply