Question Number 129731 by Adel last updated on 18/Jan/21
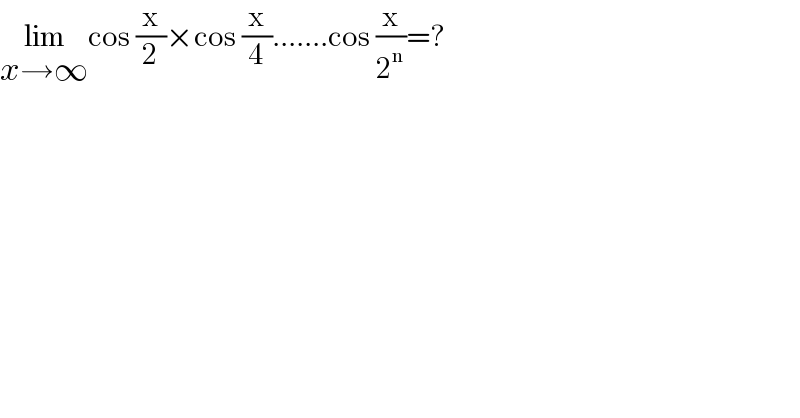
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}cos}\:\frac{\mathrm{x}}{\mathrm{2}}×\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{4}}…….\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}^{\mathrm{n}} }=? \\ $$
Answered by Dwaipayan Shikari last updated on 18/Jan/21
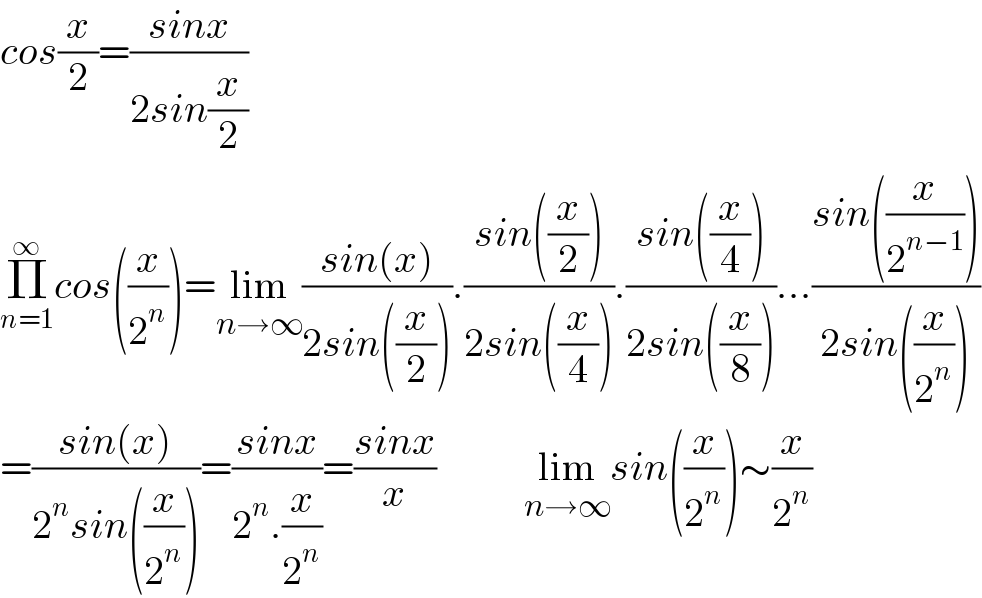
$${cos}\frac{{x}}{\mathrm{2}}=\frac{{sinx}}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}{cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{sin}\left({x}\right)}{\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{2}}\right)}.\frac{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{4}}\right)}.\frac{{sin}\left(\frac{{x}}{\mathrm{4}}\right)}{\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{8}}\right)}…\frac{{sin}\left(\frac{{x}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)}{\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)} \\ $$$$=\frac{{sin}\left({x}\right)}{\mathrm{2}^{{n}} {sin}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)}=\frac{{sinx}}{\mathrm{2}^{{n}} .\frac{{x}}{\mathrm{2}^{{n}} }}=\frac{{sinx}}{{x}}\:\:\:\:\:\:\:\:\:\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{sin}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)\sim\frac{{x}}{\mathrm{2}^{{n}} } \\ $$
Commented by Adel last updated on 18/Jan/21

$$\mathrm{tanks}\:\mathrm{bro} \\ $$
