lim-x-cos-x-cos-x-1-cos-x-

Question Number 96232 by joki last updated on 30/May/20

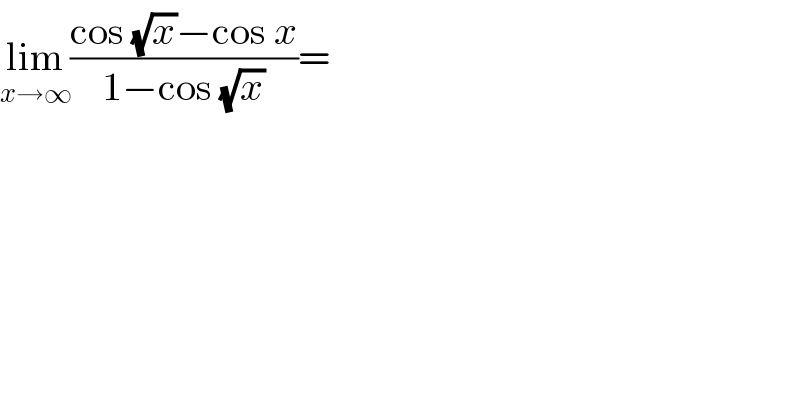
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{cos}\:\sqrt{{x}}−\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{cos}\:\sqrt{{x}}}= \\ $$

Commented by bobhans last updated on 31/May/20

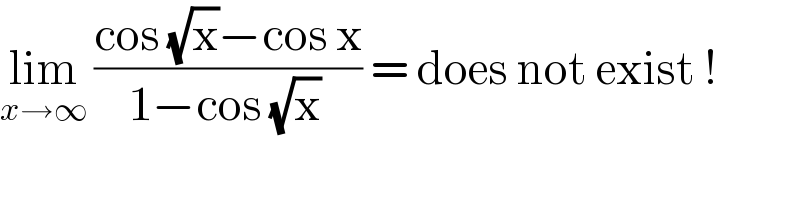
lim_(x→∞) ((cos (√x)−cos x)/(1−cos (√x) )) = does not exist !

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\sqrt{\mathrm{x}}−\mathrm{cos}\:\mathrm{x}}{\mathrm{1}−\mathrm{cos}\:\sqrt{\mathrm{x}}\:}\:=\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist}\:! \\ $$

Answered by behi83417@gmail.com last updated on 30/May/20

x=(1/t)⇒[x→∞⇒t→0] L=lim_(t→0) ((cos(√(1/t))−cost)/(1−cos(√(1/t))))=lim_(t→0) (((1−(1/(2t)))−(1−(t^2 /2)))/(1/(2t)))= =lim_(t→0) (((t^2 /2)−(1/(2t)))/(1/(2t)))=lim_(t→0) ((t^3 −1)/1)=−1 .■

$$\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\Rightarrow\left[\mathrm{x}\rightarrow\infty\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\right] \\ $$$$\mathrm{L}=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\sqrt{\frac{\mathrm{1}}{\mathrm{t}}}−\mathrm{cost}}{\mathrm{1}−\mathrm{cos}\sqrt{\frac{\mathrm{1}}{\mathrm{t}}}}=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2t}}\right)−\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right)}{\frac{\mathrm{1}}{\mathrm{2t}}}= \\ $$$$=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2t}}}{\frac{\mathrm{1}}{\mathrm{2t}}}=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{t}^{\mathrm{3}} −\mathrm{1}}{\mathrm{1}}=−\mathrm{1}\:\:.\blacksquare \\ $$

Commented by bobhans last updated on 31/May/20

$$\mathrm{no}.\:\mathrm{it}\:\mathrm{wrong} \\ $$

Answered by mathmax by abdo last updated on 31/May/20

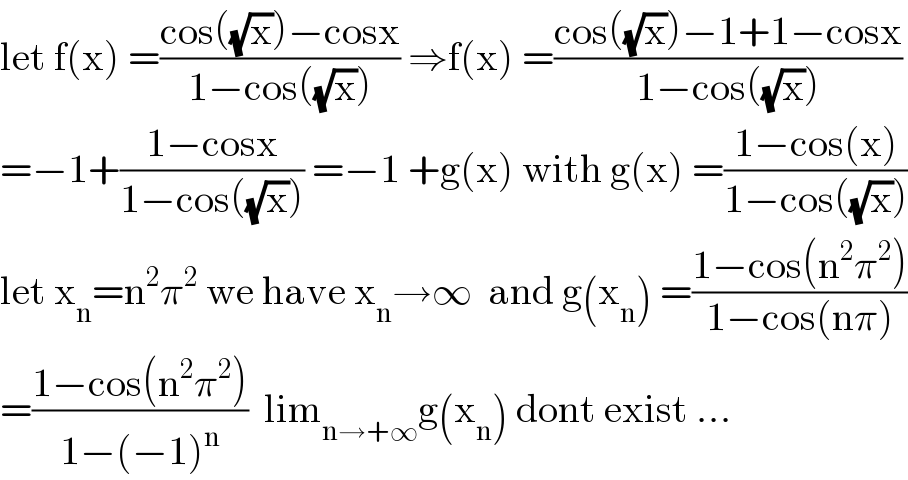
let f(x) =((cos((√x))−cosx)/(1−cos((√x)))) ⇒f(x) =((cos((√x))−1+1−cosx)/(1−cos((√x)))) =−1+((1−cosx)/(1−cos((√x)))) =−1 +g(x) with g(x) =((1−cos(x))/(1−cos((√x)))) let x_n =n^2 π^2 we have x_n →∞ and g(x_n ) =((1−cos(n^2 π^2 ))/(1−cos(nπ))) =((1−cos(n^2 π^2 ))/(1−(−1)^n )) lim_(n→+∞) g(x_n ) dont exist ...

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{cos}\left(\sqrt{\mathrm{x}}\right)−\mathrm{cosx}}{\mathrm{1}−\mathrm{cos}\left(\sqrt{\mathrm{x}}\right)}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{cos}\left(\sqrt{\mathrm{x}}\right)−\mathrm{1}+\mathrm{1}−\mathrm{cosx}}{\mathrm{1}−\mathrm{cos}\left(\sqrt{\mathrm{x}}\right)} \\ $$$$=−\mathrm{1}+\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{1}−\mathrm{cos}\left(\sqrt{\mathrm{x}}\right)}\:=−\mathrm{1}\:+\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{with}\:\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{cos}\left(\sqrt{\mathrm{x}}\right)} \\ $$$$\mathrm{let}\:\mathrm{x}_{\mathrm{n}} =\mathrm{n}^{\mathrm{2}} \pi^{\mathrm{2}} \:\mathrm{we}\:\mathrm{have}\:\mathrm{x}_{\mathrm{n}} \rightarrow\infty\:\:\mathrm{and}\:\mathrm{g}\left(\mathrm{x}_{\mathrm{n}} \right)\:=\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{n}^{\mathrm{2}} \pi^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{cos}\left(\mathrm{n}\pi\right)} \\ $$$$=\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{n}^{\mathrm{2}} \pi^{\mathrm{2}} \right)}{\mathrm{1}−\left(−\mathrm{1}\right)^{\mathrm{n}} }\:\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{g}\left(\mathrm{x}_{\mathrm{n}} \right)\:\mathrm{dont}\:\mathrm{exist}\:… \\ $$

Commented by joki last updated on 31/May/20

$${answer}\:{is}\:\mathrm{1}? \\ $$

Commented by mathmax by abdo last updated on 31/May/20

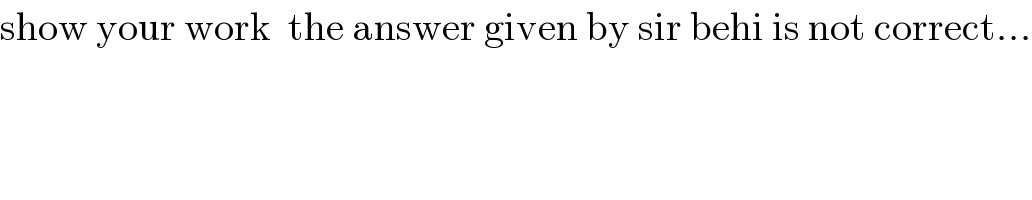
show your work the answer given by sir behi is not correct...

$$\mathrm{show}\:\mathrm{your}\:\mathrm{work}\:\:\mathrm{the}\:\mathrm{answer}\:\mathrm{given}\:\mathrm{by}\:\mathrm{sir}\:\mathrm{behi}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct}… \\ $$

Commented by joki last updated on 31/May/20

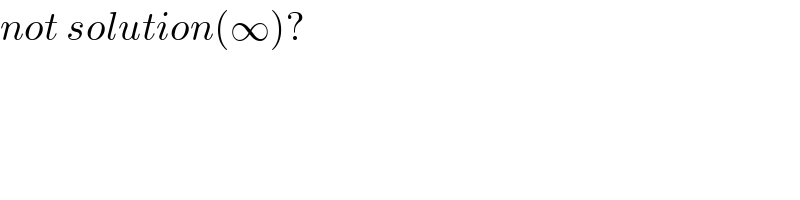
$${not}\:{solution}\left(\infty\right)? \\ $$

Answered by bemath last updated on 31/May/20

Facebook Tweet Pin

lim-x-cos-x-cos-x-1-cos-x-

Leave a Reply Cancel reply