Question Number 165392 by LEKOUMA last updated on 31/Jan/22
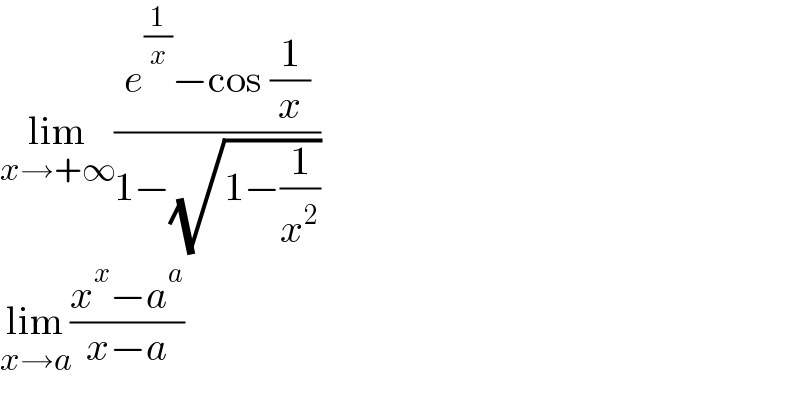
$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{{e}^{\frac{\mathrm{1}}{{x}}} −\mathrm{cos}\:\frac{\mathrm{1}}{{x}}}{\mathrm{1}−\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}} \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{x}^{{x}} −{a}^{{a}} }{{x}−{a}} \\ $$
Answered by Mathspace last updated on 31/Jan/22
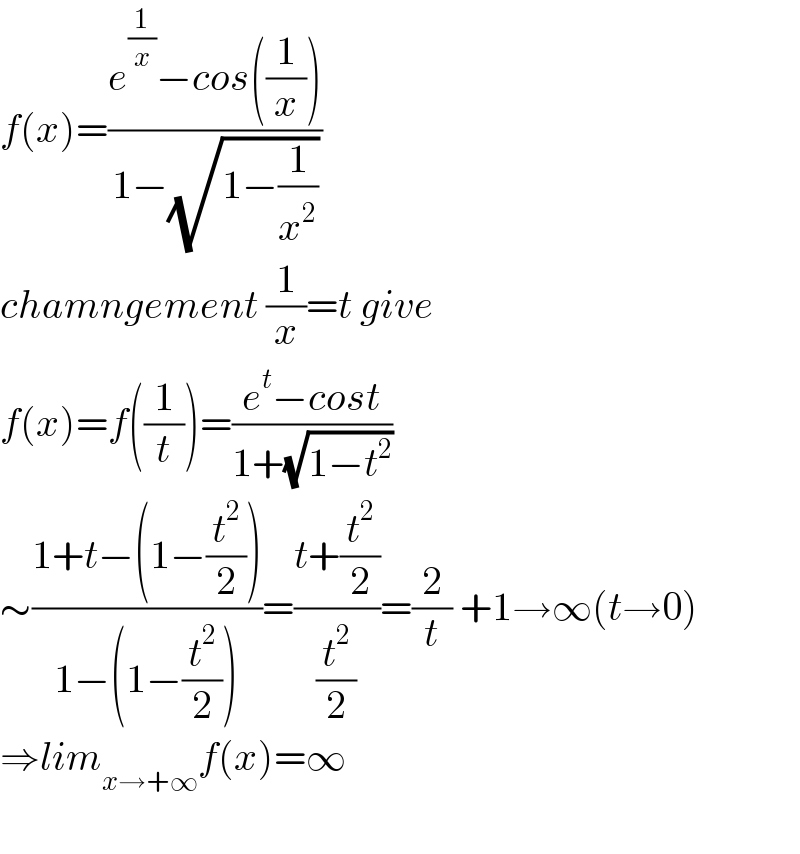
$${f}\left({x}\right)=\frac{{e}^{\frac{\mathrm{1}}{{x}}} −{cos}\left(\frac{\mathrm{1}}{{x}}\right)}{\mathrm{1}−\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}} \\ $$$${chamngement}\:\frac{\mathrm{1}}{{x}}={t}\:{give} \\ $$$${f}\left({x}\right)={f}\left(\frac{\mathrm{1}}{{t}}\right)=\frac{{e}^{{t}} −{cost}}{\mathrm{1}+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$\sim\frac{\mathrm{1}+{t}−\left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right)}{\mathrm{1}−\left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right)}=\frac{{t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}}}{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}}=\frac{\mathrm{2}}{{t}}\:+\mathrm{1}\rightarrow\infty\left({t}\rightarrow\mathrm{0}\right) \\ $$$$\Rightarrow{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)=\infty \\ $$$$ \\ $$
Answered by Mathspace last updated on 31/Jan/22
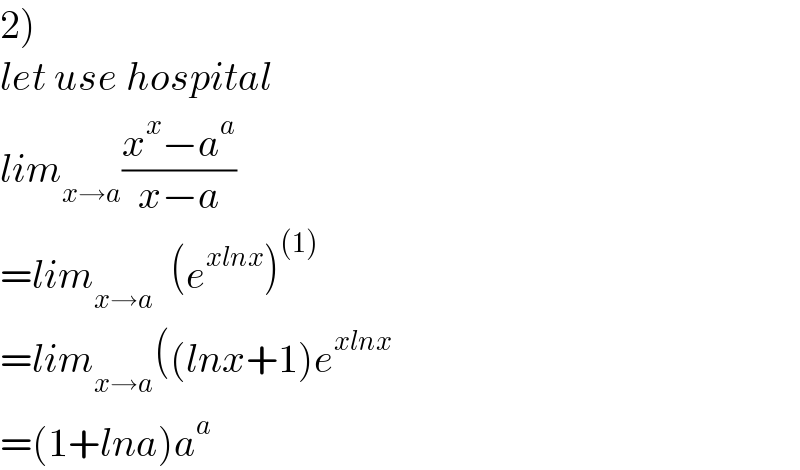
$$\left.\mathrm{2}\right) \\ $$$${let}\:{use}\:{hospital} \\ $$$${lim}_{{x}\rightarrow{a}} \frac{{x}^{{x}} −{a}^{{a}} }{{x}−{a}} \\ $$$$={lim}_{{x}\rightarrow{a}} \:\:\left({e}^{{xlnx}} \right)^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{x}\rightarrow{a}} \left(\left({lnx}+\mathrm{1}\right){e}^{{xlnx}} \right. \\ $$$$=\left(\mathrm{1}+{lna}\right){a}^{{a}} \\ $$
