Menu Close

lim-x-e-lnx-x-e-lnx-logx-

Tinku Tara 0 Comments
Pin




Question Number 102507 by Study last updated on 09/Jul/20
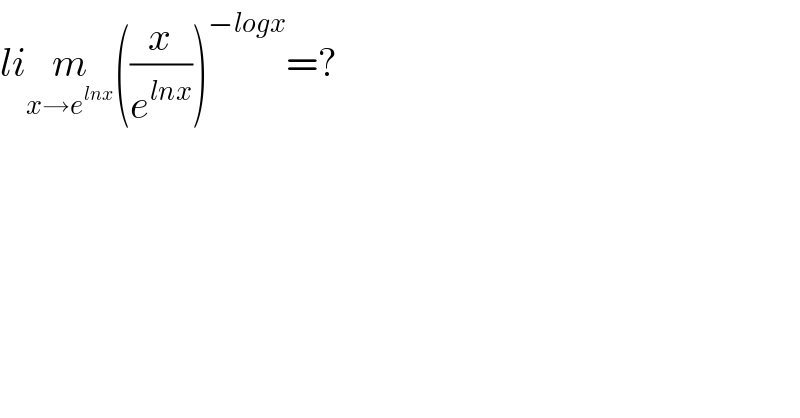
lim_(x→e^(lnx) ) ((x/e^(lnx) ))^(−logx) =?
$${li}\underset{{x}\rightarrow{e}^{{lnx}} } {{m}}\left(\frac{{x}}{{e}^{{lnx}} }\right)^{−{logx}} =? \\ $$
Commented by Study last updated on 09/Jul/20
help me
$${help}\:{me} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Jul/20
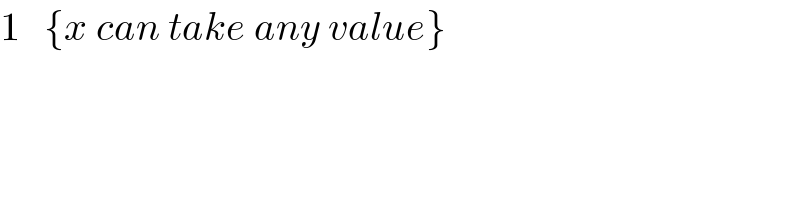
1 {x can take any value}
$$\mathrm{1}\:\:\:\left\{{x}\:{can}\:{take}\:{any}\:{value}\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *