Question Number 81558 by john santu last updated on 14/Feb/20
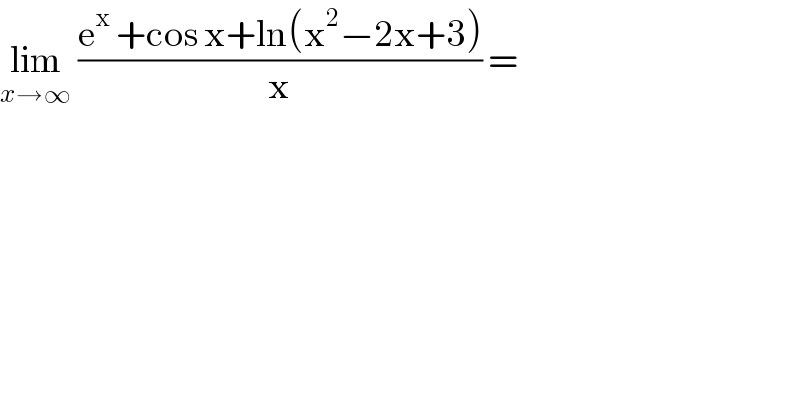
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{e}^{\mathrm{x}} \:+\mathrm{cos}\:\mathrm{x}+\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{3}\right)}{\mathrm{x}}\:=\: \\ $$
Commented by malwaan last updated on 14/Feb/20

$$\infty \\ $$
Commented by mathmax by abdo last updated on 14/Feb/20
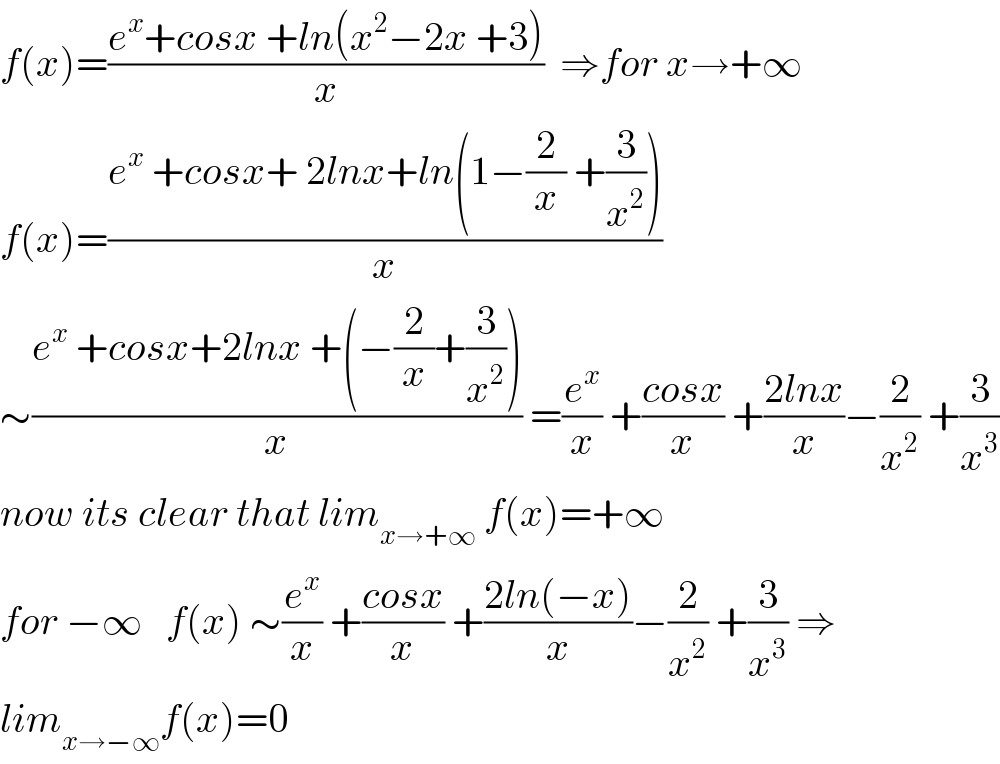
$${f}\left({x}\right)=\frac{{e}^{{x}} +{cosx}\:+{ln}\left({x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{3}\right)}{{x}}\:\:\Rightarrow{for}\:{x}\rightarrow+\infty \\ $$$${f}\left({x}\right)=\frac{{e}^{{x}} \:+{cosx}+\:\mathrm{2}{lnx}+{ln}\left(\mathrm{1}−\frac{\mathrm{2}}{{x}}\:+\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)}{{x}} \\ $$$$\sim\frac{{e}^{{x}} \:+{cosx}+\mathrm{2}{lnx}\:+\left(−\frac{\mathrm{2}}{{x}}+\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)}{{x}}\:=\frac{{e}^{{x}} }{{x}}\:+\frac{{cosx}}{{x}}\:+\frac{\mathrm{2}{lnx}}{{x}}−\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{3}}{{x}^{\mathrm{3}} } \\ $$$${now}\:{its}\:{clear}\:{that}\:{lim}_{{x}\rightarrow+\infty} \:{f}\left({x}\right)=+\infty \\ $$$${for}\:−\infty\:\:\:{f}\left({x}\right)\:\sim\frac{{e}^{{x}} }{{x}}\:+\frac{{cosx}}{{x}}\:+\frac{\mathrm{2}{ln}\left(−{x}\right)}{{x}}−\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{3}}{{x}^{\mathrm{3}} }\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow−\infty} {f}\left({x}\right)=\mathrm{0} \\ $$
