Question Number 63964 by meme last updated on 11/Jul/19
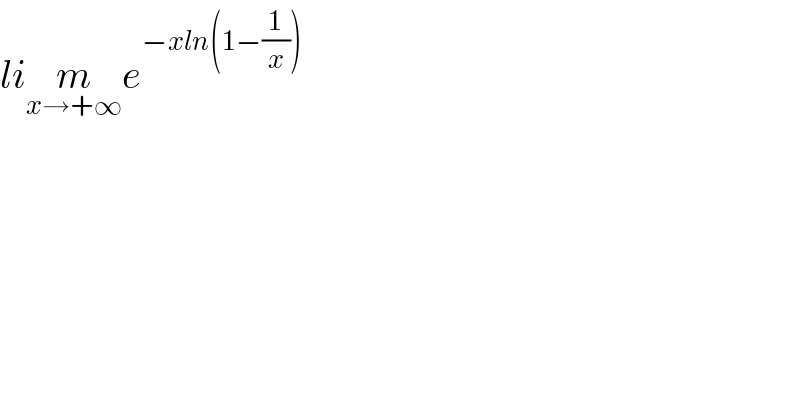
$${li}\underset{{x}\rightarrow+\infty} {{m}e}^{−{xln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)} \\ $$
Commented by Prithwish sen last updated on 11/Jul/19

$$\mathrm{li}\underset{\mathrm{x}\rightarrow\infty} {\mathrm{m}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{x}} \rightarrow\:\mathrm{e}^{−\mathrm{1}} \\ $$
Commented by turbo msup by abdo last updated on 12/Jul/19
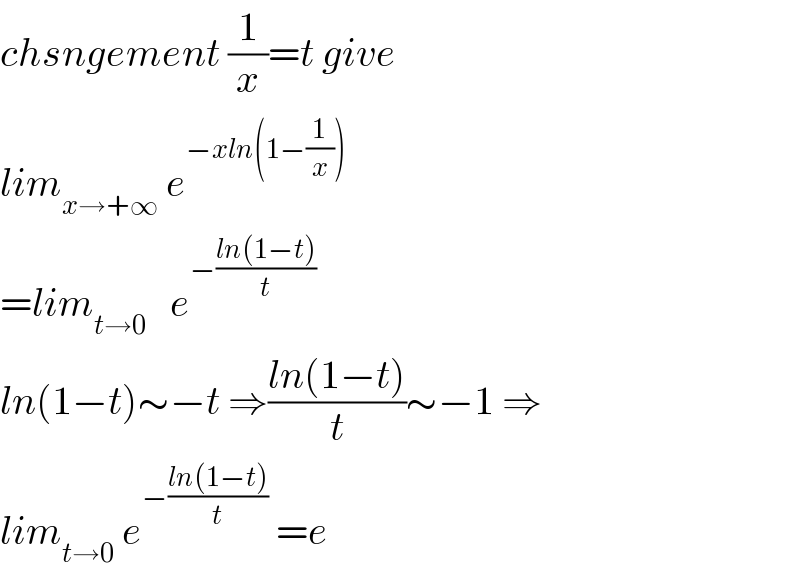
$${chsngement}\:\frac{\mathrm{1}}{{x}}={t}\:{give} \\ $$$${lim}_{{x}\rightarrow+\infty} \:{e}^{−{xln}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:{e}^{−\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}} \\ $$$${ln}\left(\mathrm{1}−{t}\right)\sim−{t}\:\Rightarrow\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}\sim−\mathrm{1}\:\Rightarrow \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} \:{e}^{−\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}} \:={e} \\ $$
