Question Number 181104 by cortano1 last updated on 21/Nov/22
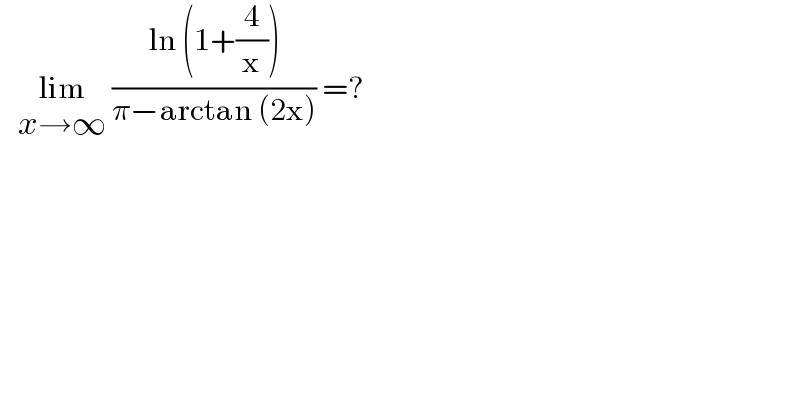
$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{x}}\right)}{\pi−\mathrm{arctan}\:\left(\mathrm{2x}\right)}\:=?\: \\ $$
Commented by Frix last updated on 21/Nov/22
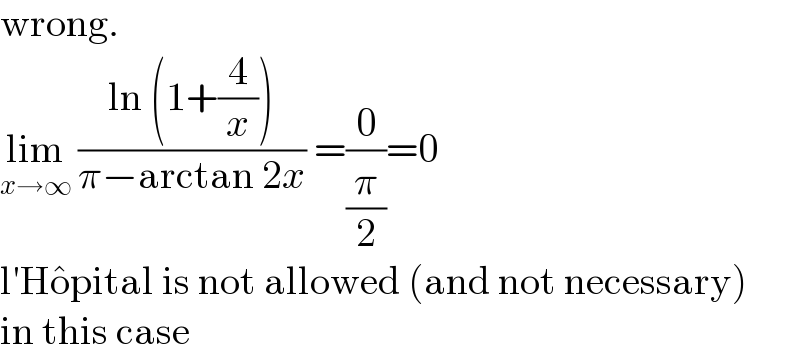
$$\mathrm{wrong}. \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{4}}{{x}}\right)}{\pi−\mathrm{arctan}\:\mathrm{2}{x}}\:=\frac{\mathrm{0}}{\frac{\pi}{\mathrm{2}}}=\mathrm{0} \\ $$$$\mathrm{l}'\mathrm{H}\hat {\mathrm{o}pital}\:\mathrm{is}\:\mathrm{not}\:\mathrm{allowed}\:\left(\mathrm{and}\:\mathrm{not}\:\mathrm{necessary}\right) \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$
Answered by a.lgnaoui last updated on 21/Nov/22
![f(x)=((ln(1+(4/x)))/(π−arctan (2x))) x→∞ arctan (2x) →(π/2) lim_(x→∞) f(x)=(2/π) lim_(x→∞) [ln(1+(4/x))]=(2/π)×ln(1) lim_(x→∞) ((ln(1+(4/x)))/(π−arctan(2x)))=0](https://www.tinkutara.com/question/Q181117.png)
$${f}\left({x}\right)=\frac{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{x}}\right)}{\pi−\mathrm{arctan}\:\left(\mathrm{2x}\right)} \\ $$$$\mathrm{x}\rightarrow\infty\:\:\mathrm{arctan}\:\left(\mathrm{2x}\right)\:\rightarrow\frac{\pi}{\mathrm{2}}\: \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\infty} {f}\left({x}\right)=\frac{\mathrm{2}}{\pi}\:\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \left[\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{x}}\right)\right]=\frac{\mathrm{2}}{\pi}×\mathrm{ln}\left(\mathrm{1}\right) \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \frac{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{x}}\right)}{\pi−\mathrm{arctan}\left(\mathrm{2x}\right)}=\mathrm{0} \\ $$$$ \\ $$
Answered by Gamil last updated on 21/Nov/22
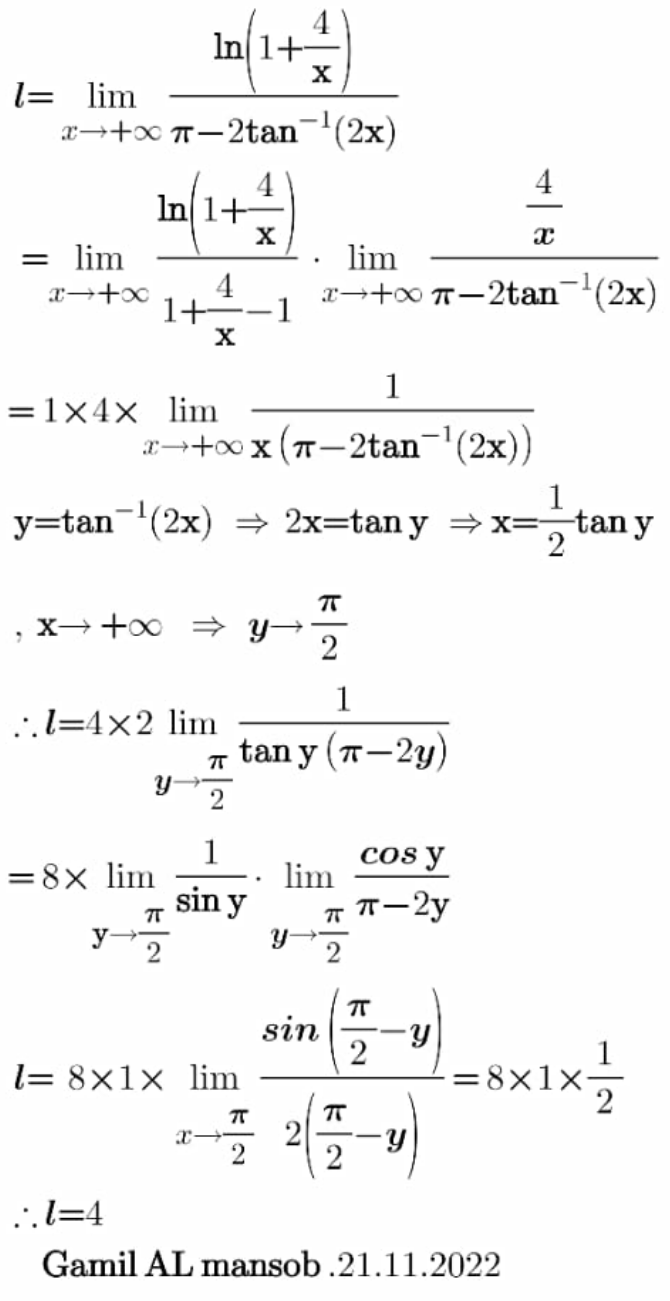
Commented by Frix last updated on 21/Nov/22

$$\mathrm{wrong}. \\ $$
