Question Number 103655 by Study last updated on 16/Jul/20
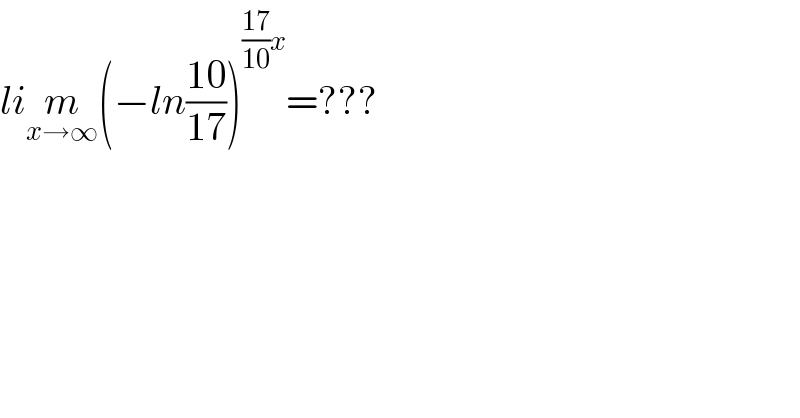
$${li}\underset{{x}\rightarrow\infty} {{m}}\left(−{ln}\frac{\mathrm{10}}{\mathrm{17}}\right)^{\frac{\mathrm{17}}{\mathrm{10}}{x}} =??? \\ $$
Commented by JDamian last updated on 16/Jul/20

$$\infty \\ $$
Commented by Study last updated on 16/Jul/20
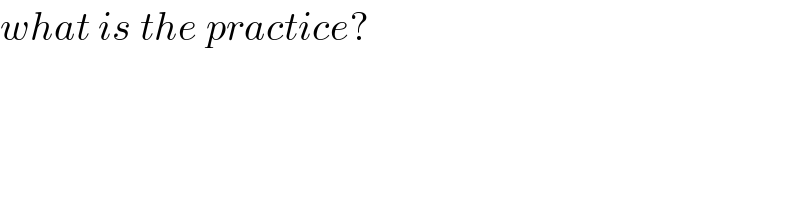
$${what}\:{is}\:{the}\:{practice}? \\ $$
Commented by Worm_Tail last updated on 16/Jul/20
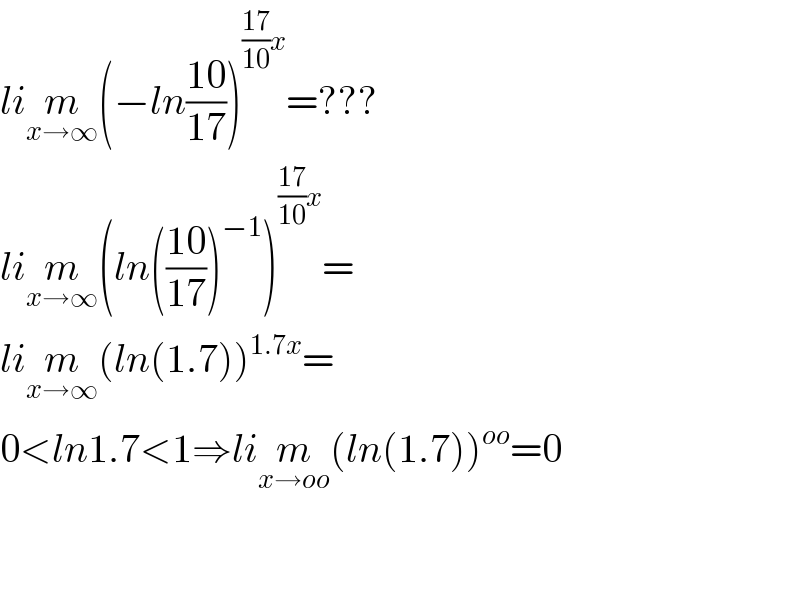
$${li}\underset{{x}\rightarrow\infty} {{m}}\left(−{ln}\frac{\mathrm{10}}{\mathrm{17}}\right)^{\frac{\mathrm{17}}{\mathrm{10}}{x}} =??? \\ $$$${li}\underset{{x}\rightarrow\infty} {{m}}\left({ln}\left(\frac{\mathrm{10}}{\mathrm{17}}\right)^{−\mathrm{1}} \right)^{\frac{\mathrm{17}}{\mathrm{10}}{x}} = \\ $$$${li}\underset{{x}\rightarrow\infty} {{m}}\left({ln}\left(\mathrm{1}.\mathrm{7}\right)\right)^{\mathrm{1}.\mathrm{7}{x}} = \\ $$$$\mathrm{0}<{ln}\mathrm{1}.\mathrm{7}<\mathrm{1}\Rightarrow{li}\underset{{x}\rightarrow{oo}} {{m}}\left({ln}\left(\mathrm{1}.\mathrm{7}\right)\right)^{{oo}} =\mathrm{0} \\ $$$$\:\:\:\: \\ $$$$ \\ $$
