Question Number 92289 by jagoll last updated on 06/May/20
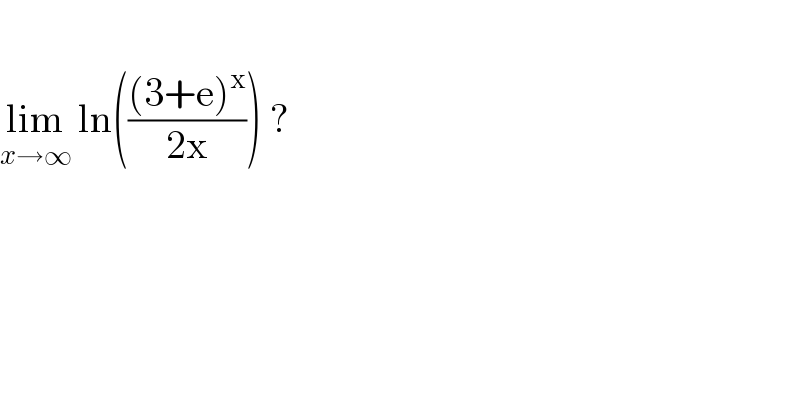
$$ \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{ln}\left(\frac{\left(\mathrm{3}+\mathrm{e}\right)^{\mathrm{x}} }{\mathrm{2x}}\right)\:? \\ $$
Commented by mathmax by abdo last updated on 06/May/20
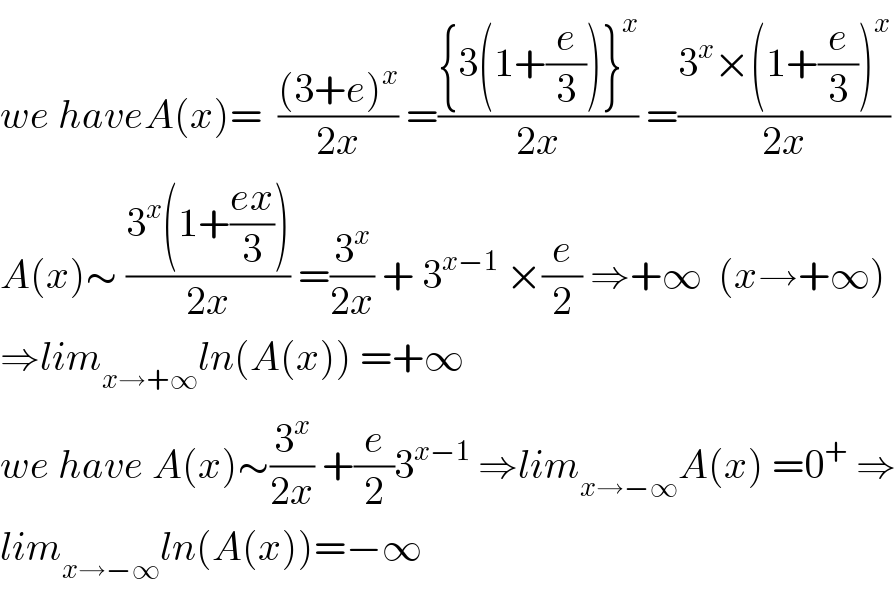
$${we}\:{haveA}\left({x}\right)=\:\:\frac{\left(\mathrm{3}+{e}\right)^{{x}} }{\mathrm{2}{x}}\:=\frac{\left\{\mathrm{3}\left(\mathrm{1}+\frac{{e}}{\mathrm{3}}\right)\right\}^{{x}} }{\mathrm{2}{x}}\:=\frac{\mathrm{3}^{{x}} ×\left(\mathrm{1}+\frac{{e}}{\mathrm{3}}\right)^{{x}} }{\mathrm{2}{x}} \\ $$$${A}\left({x}\right)\sim\:\frac{\mathrm{3}^{{x}} \left(\mathrm{1}+\frac{{ex}}{\mathrm{3}}\right)}{\mathrm{2}{x}}\:=\frac{\mathrm{3}^{{x}} }{\mathrm{2}{x}}\:+\:\mathrm{3}^{{x}−\mathrm{1}} \:×\frac{{e}}{\mathrm{2}}\:\Rightarrow+\infty\:\:\left({x}\rightarrow+\infty\right) \\ $$$$\Rightarrow{lim}_{{x}\rightarrow+\infty} {ln}\left({A}\left({x}\right)\right)\:=+\infty \\ $$$${we}\:{have}\:{A}\left({x}\right)\sim\frac{\mathrm{3}^{{x}} }{\mathrm{2}{x}}\:+\frac{{e}}{\mathrm{2}}\mathrm{3}^{{x}−\mathrm{1}} \:\Rightarrow{lim}_{{x}\rightarrow−\infty} {A}\left({x}\right)\:=\mathrm{0}^{+} \:\Rightarrow \\ $$$${lim}_{{x}\rightarrow−\infty} {ln}\left({A}\left({x}\right)\right)=−\infty \\ $$
