Question Number 93821 by john santu last updated on 15/May/20
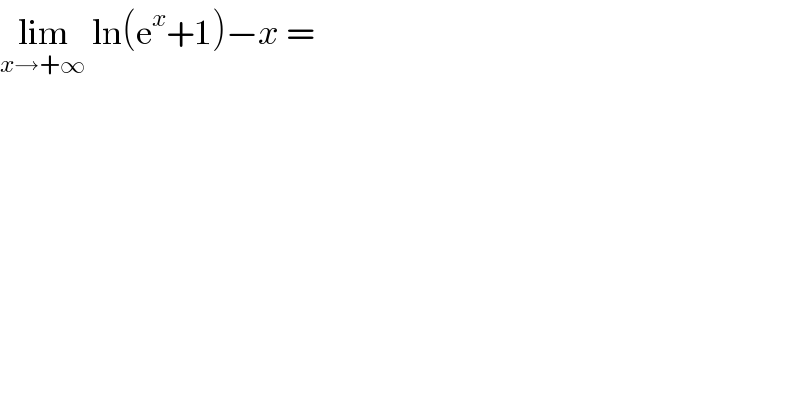
$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\mathrm{ln}\left(\mathrm{e}^{{x}} +\mathrm{1}\right)−{x}\:=\: \\ $$
Commented by JDamian last updated on 15/May/20

$$\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 15/May/20
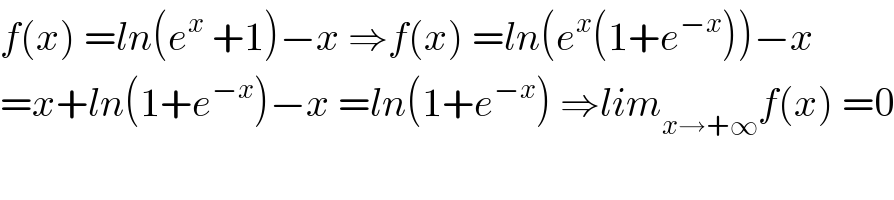
$${f}\left({x}\right)\:={ln}\left({e}^{{x}} \:+\mathrm{1}\right)−{x}\:\Rightarrow{f}\left({x}\right)\:={ln}\left({e}^{{x}} \left(\mathrm{1}+{e}^{−{x}} \right)\right)−{x} \\ $$$$={x}+{ln}\left(\mathrm{1}+{e}^{−{x}} \right)−{x}\:={ln}\left(\mathrm{1}+{e}^{−{x}} \right)\:\Rightarrow{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)\:=\mathrm{0} \\ $$
Commented by Kunal12588 last updated on 15/May/20
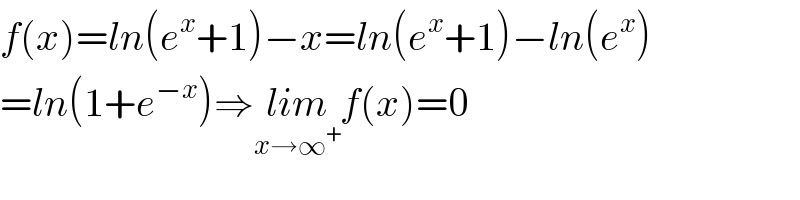
$${f}\left({x}\right)={ln}\left({e}^{{x}} +\mathrm{1}\right)−{x}={ln}\left({e}^{{x}} +\mathrm{1}\right)−{ln}\left({e}^{{x}} \right) \\ $$$$={ln}\left(\mathrm{1}+{e}^{−{x}} \right)\Rightarrow\underset{{x}\rightarrow\infty^{+} } {{lim}f}\left({x}\right)=\mathrm{0} \\ $$
Answered by john santu last updated on 15/May/20

