Question Number 120201 by bemath last updated on 30/Oct/20
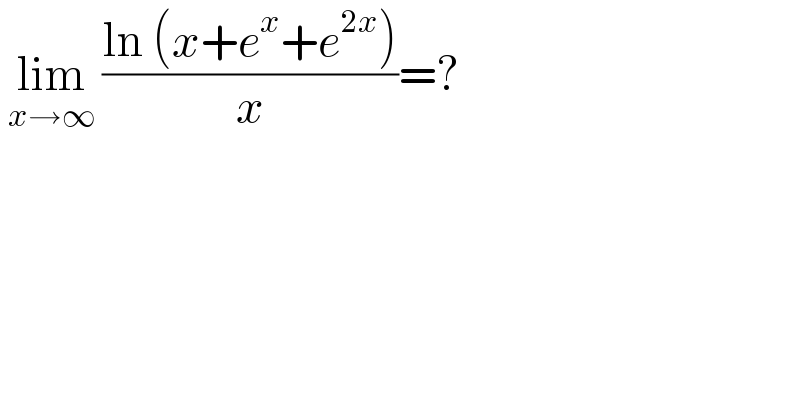
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left({x}+{e}^{{x}} +{e}^{\mathrm{2}{x}} \right)}{{x}}=? \\ $$
Answered by benjo_mathlover last updated on 30/Oct/20
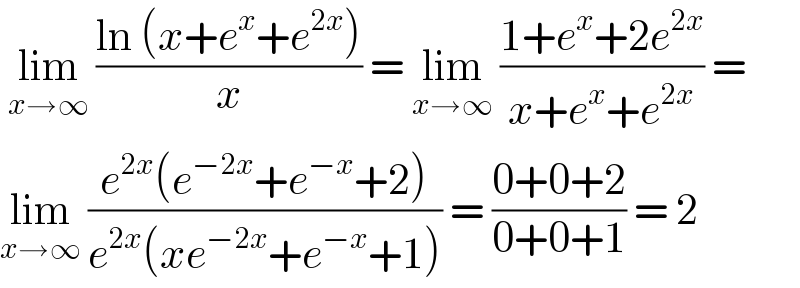
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left({x}+{e}^{{x}} +{e}^{\mathrm{2}{x}} \right)}{{x}}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}+{e}^{{x}} +\mathrm{2}{e}^{\mathrm{2}{x}} }{{x}+{e}^{{x}} +{e}^{\mathrm{2}{x}} }\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{e}^{\mathrm{2}{x}} \left({e}^{−\mathrm{2}{x}} +{e}^{−{x}} +\mathrm{2}\right)}{{e}^{\mathrm{2}{x}} \left({xe}^{−\mathrm{2}{x}} +{e}^{−{x}} +\mathrm{1}\right)}\:=\:\frac{\mathrm{0}+\mathrm{0}+\mathrm{2}}{\mathrm{0}+\mathrm{0}+\mathrm{1}}\:=\:\mathrm{2} \\ $$
Answered by Dwaipayan Shikari last updated on 30/Oct/20
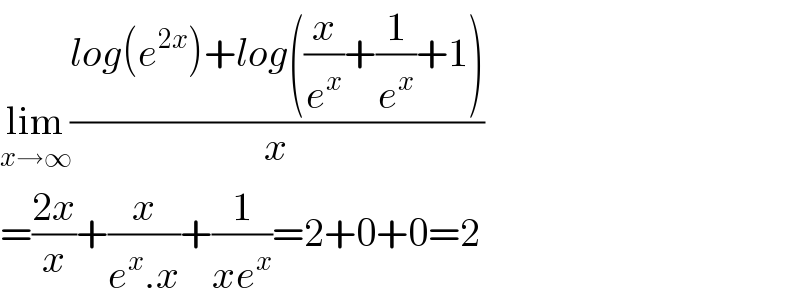
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{log}\left({e}^{\mathrm{2}{x}} \right)+{log}\left(\frac{{x}}{{e}^{{x}} }+\frac{\mathrm{1}}{{e}^{{x}} }+\mathrm{1}\right)}{{x}} \\ $$$$=\frac{\mathrm{2}{x}}{{x}}+\frac{{x}}{{e}^{{x}} .{x}}+\frac{\mathrm{1}}{{xe}^{{x}} }=\mathrm{2}+\mathrm{0}+\mathrm{0}=\mathrm{2} \\ $$
