Question Number 92577 by jagoll last updated on 08/May/20

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\mathrm{x}}{\mathrm{x}} \\ $$
Commented by Tony Lin last updated on 08/May/20
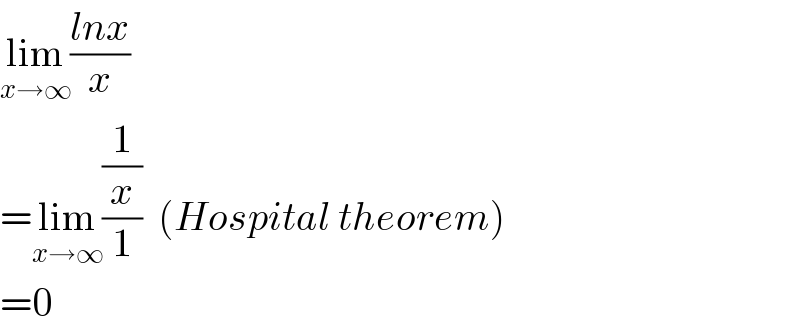
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{lnx}}{{x}} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{{x}}}{\mathrm{1}}\:\:\left({Hospital}\:{theorem}\right) \\ $$$$=\mathrm{0} \\ $$
Commented by jagoll last updated on 08/May/20

$$\mathrm{thank}\:\mathrm{you}. \\ $$$$\mathrm{1}\:\mathrm{way}\:\mathrm{via}\:\mathrm{L}'\mathrm{Hopital}\: \\ $$$$\mathrm{1}\:\mathrm{way}\:\mathrm{via}\:\mathrm{squeeze}\:\mathrm{theorem}\: \\ $$
Commented by turbo msup by abdo last updated on 08/May/20
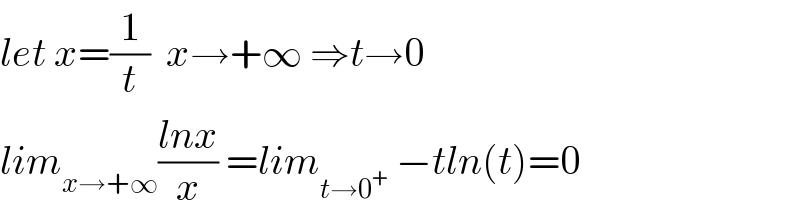
$${let}\:{x}=\frac{\mathrm{1}}{{t}}\:\:{x}\rightarrow+\infty\:\Rightarrow{t}\rightarrow\mathrm{0}\: \\ $$$${lim}_{{x}\rightarrow+\infty} \frac{{lnx}}{{x}}\:={lim}_{{t}\rightarrow\mathrm{0}^{+} } \:−{tln}\left({t}\right)=\mathrm{0} \\ $$
Answered by john santu last updated on 08/May/20

$$\Rightarrow\mathrm{ln}\left(\mathrm{x}\right)\:=\:\int_{\mathrm{1}} ^{\:{x}} \frac{\mathrm{1}}{\mathrm{t}}\:\mathrm{dt}\:\leqslant\:\int\underset{\mathrm{1}} {\overset{\:\mathrm{x}} {\:}}\mathrm{1}\:\mathrm{dt}\: \\ $$$$\mathrm{ln}\left(\mathrm{x}\right)\:\leqslant\:\mathrm{x}\:,\:\forall\mathrm{x}\:\geqslant\:\mathrm{1}\: \\ $$$$\mathrm{ln}\left(\sqrt{\mathrm{x}}\right)\:\leqslant\sqrt{\mathrm{x}}\: \\ $$$$\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{2}}\leqslant\:\sqrt{\mathrm{x}}\:\Rightarrow\mathrm{ln}\left(\mathrm{x}\right)\leqslant\mathrm{2}\sqrt{\mathrm{x}} \\ $$$$\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}}\:\leqslant\:\frac{\mathrm{2}\sqrt{\mathrm{x}}}{\mathrm{x}}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{x}}}\: \\ $$$$\mathrm{by}\:\mathrm{squeeze}\:\mathrm{theorem}\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}}\:\leqslant\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{x}}}\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}}\:=\:\mathrm{0} \\ $$
