Question Number 34843 by rahul 19 last updated on 11/May/18

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}_{} }\:\frac{\mathrm{ln}\:{x}}{{x}}\:=\:? \\ $$$${You}\:{can}\:\:{only}\:{use} \\ $$$${series}\:{expansion}\:/\:{sandwich}\:{theorem}! \\ $$
Commented by abdo mathsup 649 cc last updated on 11/May/18
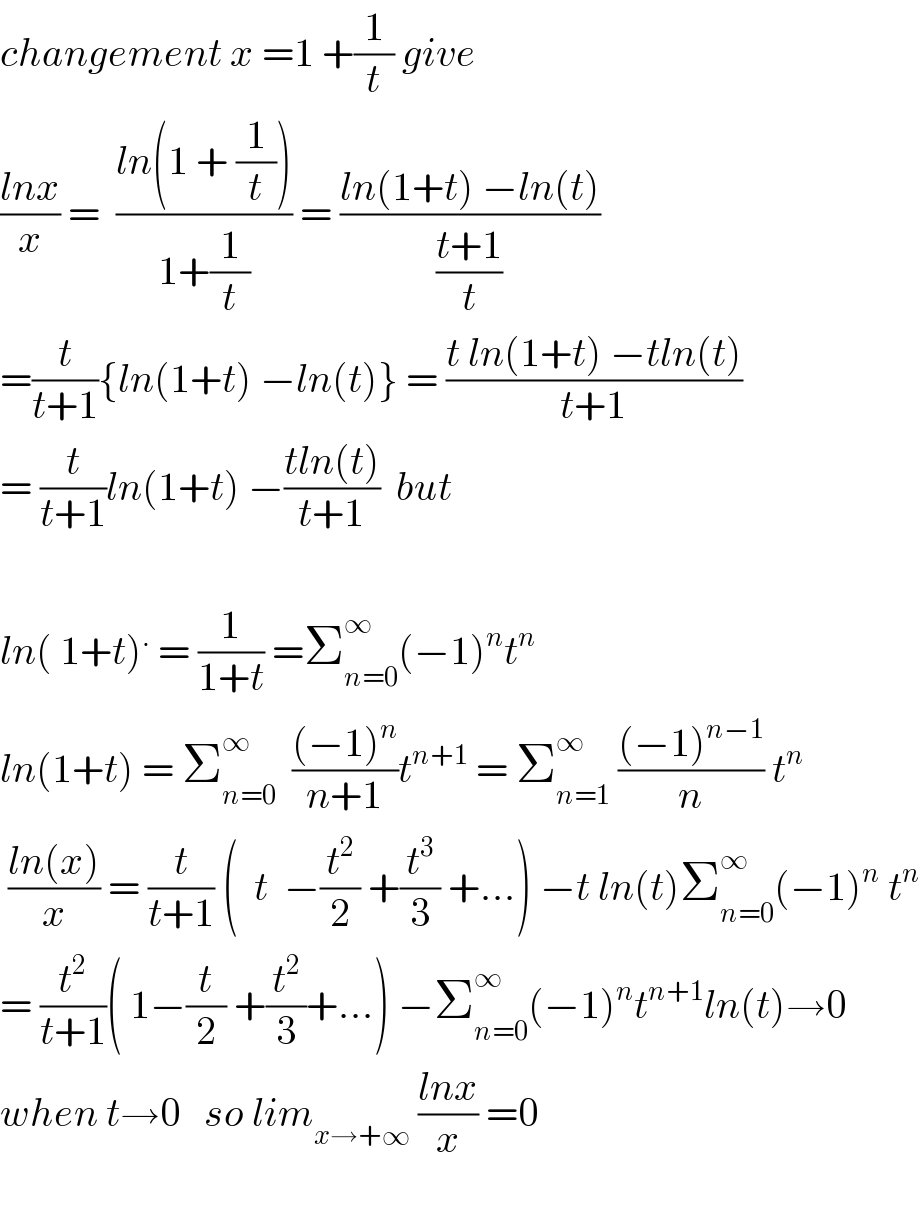
$${changement}\:{x}\:=\mathrm{1}\:+\frac{\mathrm{1}}{{t}}\:{give}\:\: \\ $$$$\frac{{lnx}}{{x}}\:=\:\:\frac{{ln}\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{t}}\right)}{\mathrm{1}+\frac{\mathrm{1}}{{t}}}\:=\:\frac{{ln}\left(\mathrm{1}+{t}\right)\:−{ln}\left({t}\right)}{\frac{{t}+\mathrm{1}}{{t}}} \\ $$$$=\frac{{t}}{{t}+\mathrm{1}}\left\{{ln}\left(\mathrm{1}+{t}\right)\:−{ln}\left({t}\right)\right\}\:=\:\frac{{t}\:{ln}\left(\mathrm{1}+{t}\right)\:−{tln}\left({t}\right)}{{t}+\mathrm{1}} \\ $$$$=\:\frac{{t}}{{t}+\mathrm{1}}{ln}\left(\mathrm{1}+{t}\right)\:−\frac{{tln}\left({t}\right)}{{t}+\mathrm{1}}\:\:{but} \\ $$$$ \\ $$$${ln}\left(\:\mathrm{1}+{t}\right)^{.} \:=\:\frac{\mathrm{1}}{\mathrm{1}+{t}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {t}^{{n}} \\ $$$${ln}\left(\mathrm{1}+{t}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{t}^{{n}+\mathrm{1}} \:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{t}^{{n}} \\ $$$$\:\frac{{ln}\left({x}\right)}{{x}}\:=\:\frac{{t}}{{t}+\mathrm{1}}\:\left(\:\:{t}\:\:−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\:+…\right)\:−{t}\:{ln}\left({t}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{t}^{{n}} \\ $$$$=\:\frac{{t}^{\mathrm{2}} }{{t}+\mathrm{1}}\left(\:\mathrm{1}−\frac{{t}}{\mathrm{2}}\:+\frac{{t}^{\mathrm{2}} }{\mathrm{3}}+…\right)\:−\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {t}^{{n}+\mathrm{1}} {ln}\left({t}\right)\rightarrow\mathrm{0} \\ $$$${when}\:{t}\rightarrow\mathrm{0}\:\:\:{so}\:{lim}_{{x}\rightarrow+\infty} \:\frac{{lnx}}{{x}}\:=\mathrm{0} \\ $$$$ \\ $$
