Question Number 28098 by tawa tawa last updated on 20/Jan/18
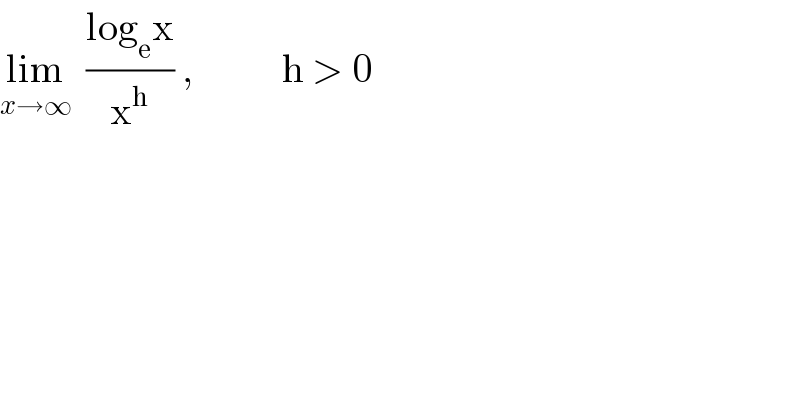
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\frac{\mathrm{log}_{\mathrm{e}} \mathrm{x}}{\mathrm{x}^{\mathrm{h}} }\:,\:\:\:\:\:\:\:\:\:\:\:\mathrm{h}\:>\:\mathrm{0} \\ $$
Answered by ajfour last updated on 20/Jan/18
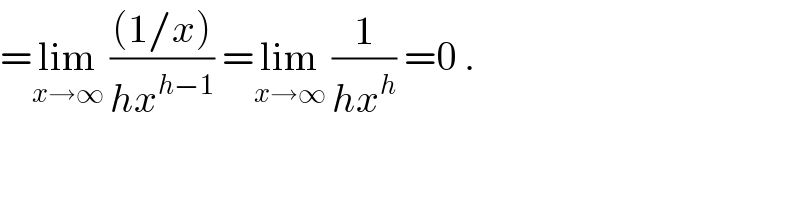
$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{1}/{x}\right)}{{hx}^{{h}−\mathrm{1}} }\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{hx}^{{h}} }\:=\mathrm{0}\:. \\ $$
Commented by tawa tawa last updated on 21/Jan/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
