Question Number 168256 by mathlove last updated on 07/Apr/22
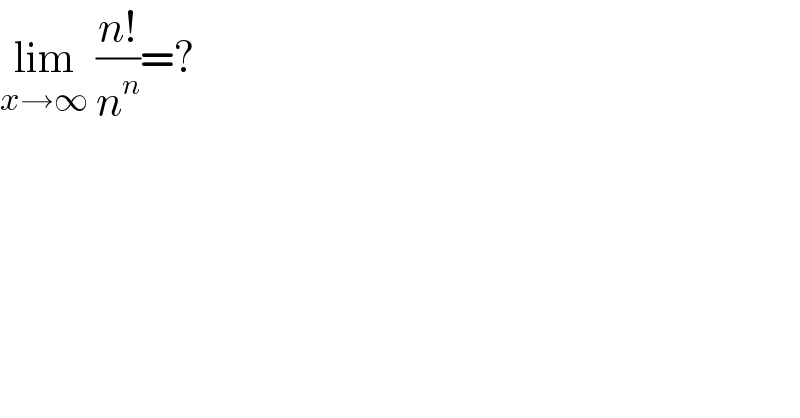
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{n}!}{{n}^{{n}} }=? \\ $$
Answered by MJS_new last updated on 07/Apr/22
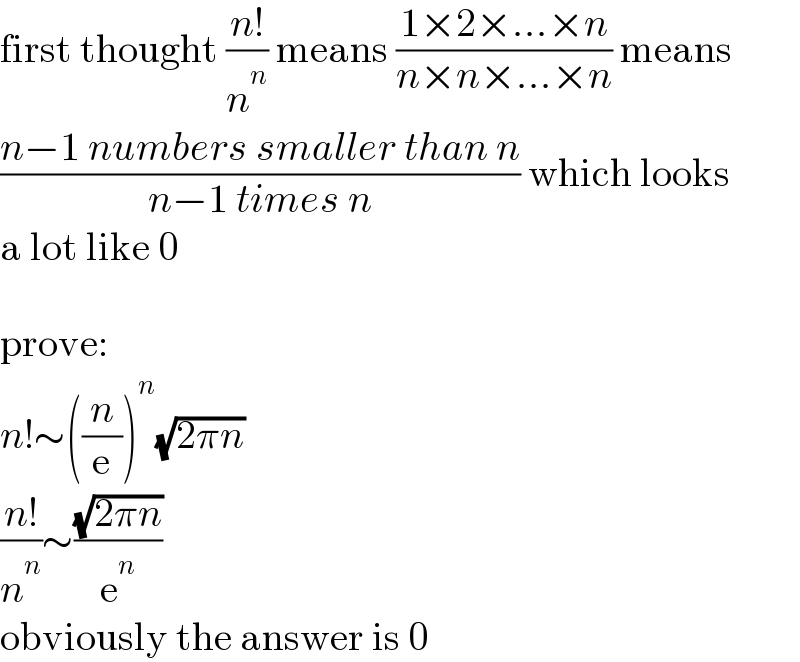
$$\mathrm{first}\:\mathrm{thought}\:\frac{{n}!}{{n}^{{n}} }\:\mathrm{means}\:\frac{\mathrm{1}×\mathrm{2}×…×{n}}{{n}×{n}×…×{n}}\:\mathrm{means} \\ $$$$\frac{{n}−\mathrm{1}\:{numbers}\:{smaller}\:{than}\:{n}}{{n}−\mathrm{1}\:{times}\:{n}}\:\mathrm{which}\:\mathrm{looks} \\ $$$$\mathrm{a}\:\mathrm{lot}\:\mathrm{like}\:\mathrm{0} \\ $$$$ \\ $$$$\mathrm{prove}: \\ $$$${n}!\sim\left(\frac{{n}}{\mathrm{e}}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}} \\ $$$$\frac{{n}!}{{n}^{{n}} }\sim\frac{\sqrt{\mathrm{2}\pi{n}}}{\mathrm{e}^{{n}} } \\ $$$$\mathrm{obviously}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{0} \\ $$
