Question Number 155710 by SANOGO last updated on 03/Oct/21
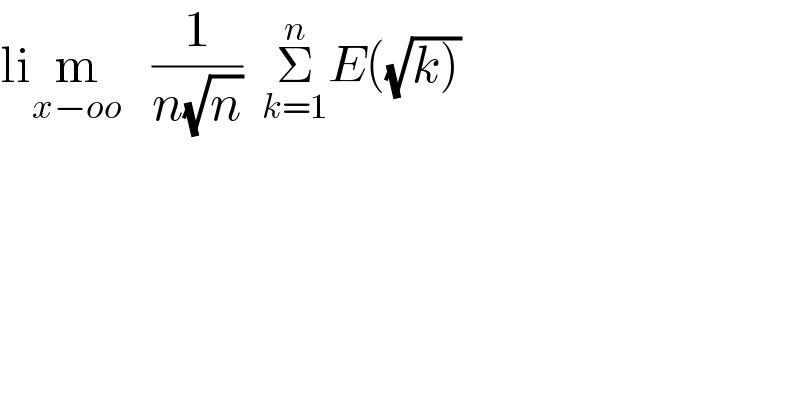
$$\mathrm{li}\underset{{x}−{oo}} {\mathrm{m}}\:\:\:\frac{\mathrm{1}}{{n}\sqrt{{n}}}\:\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{E}\left(\sqrt{\left.{k}\right)}\right. \\ $$$$ \\ $$
Commented by yeti123 last updated on 03/Oct/21
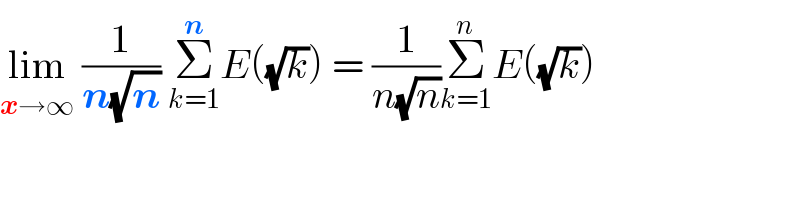
$$\underset{\boldsymbol{{x}}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\boldsymbol{{n}}\sqrt{\boldsymbol{{n}}}}\:\underset{{k}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}{E}\left(\sqrt{{k}}\right)\:=\:\frac{\mathrm{1}}{{n}\sqrt{{n}}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{E}\left(\sqrt{{k}}\right) \\ $$
Answered by puissant last updated on 03/Oct/21

$$\mathscr{L}\:\:=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}\sqrt{{n}}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{E}\left(\sqrt{{k}}\right) \\ $$$$\:\mathscr{L}\:=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{n}}}{E}\left(\sqrt{{k}}\right) \\ $$$$=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{E}\left(\sqrt{\frac{{k}}{{n}}}\right) \\ $$$${Qui}\:{est}\:{sous}\:{la}\:{forme}\:\frac{{b}−{a}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{f}\left({a}+{k}\frac{{b}−{a}}{{n}}\right) \\ $$$${il}\:{s}'{agit}\:{de}\:{la}\:{somme}\:{de}\:{riemann}\:{on}\:{a}\:{donc}\:: \\ $$$$\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:\frac{{b}−{a}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{f}\left({a}+{k}\frac{{b}−{a}}{{n}}\right)=\int_{{a}} ^{{b}} {f}\left({x}\right){dx} \\ $$$$\Rightarrow\:\mathscr{L}=\int_{\mathrm{0}} ^{\mathrm{1}} {E}\left({x}\right){dx}=\mathrm{0}\left(\mathrm{1}−\mathrm{0}\right)=\mathrm{0}.. \\ $$$$\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\therefore\because\:\:\mathscr{L}=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}\sqrt{{n}}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{E}\left(\sqrt{{k}}\right)=\mathrm{0}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:………..\mathscr{L}{e}\:{puissant}……….. \\ $$
Commented by SANOGO last updated on 03/Oct/21
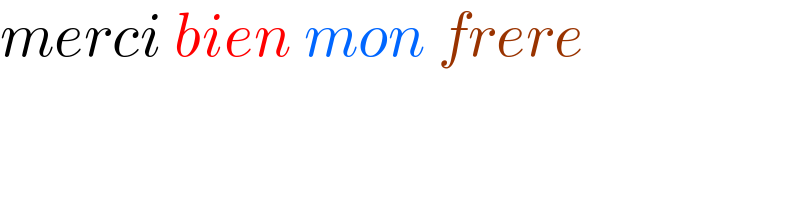
$${merci}\:{bien}\:{mon}\:{frere} \\ $$
Commented by Kamel last updated on 04/Oct/21
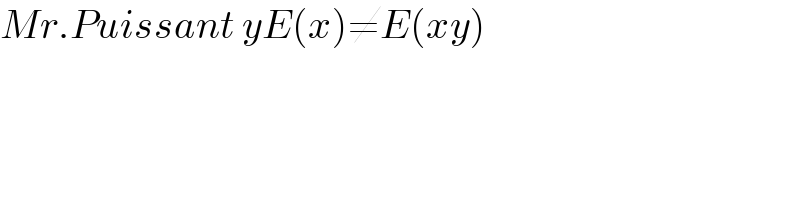
$${Mr}.{Puissant}\:{yE}\left({x}\right)\neq{E}\left({xy}\right) \\ $$
Commented by puissant last updated on 04/Oct/21
$${Thanks}\:{Mr}\:{Kamel}.. \\ $$$${Mr}\:{Sanogo}\:{Desol}\acute {{e}e}.. \\ $$
Answered by Kamel last updated on 04/Oct/21
![S_n =Σ_(k=1) ^n [(√k)]=Σ_(k=1) ^n (√k)−Σ_(k=1) ^n {(√k)} ∀1≤k≤n 0≤ Σ_(k=1) ^n {(√k)}<n ⇒0≤(1/( n(√n)))Σ_(k=1) ^n {(√k)}<(1/( (√n))) ∴ lim_(n→+∞) (1/(n(√n)))Σ_(k=1) ^n [(√k)]=lim_(n→+∞) (1/n)Σ_(k=1) ^n (√(k/n))=∫_0 ^1 (√x)dx =(2/3)](https://www.tinkutara.com/question/Q155732.png)
$${S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\sqrt{{k}}\right]=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\sqrt{{k}}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left\{\sqrt{{k}}\right\} \\ $$$$\forall\mathrm{1}\leqslant{k}\leqslant{n}\:\:\mathrm{0}\leqslant\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left\{\sqrt{{k}}\right\}<{n}\:\Rightarrow\mathrm{0}\leqslant\frac{\mathrm{1}}{\:{n}\sqrt{{n}}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left\{\sqrt{{k}}\right\}<\frac{\mathrm{1}}{\:\sqrt{{n}}} \\ $$$$\therefore\:\:\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{{n}\sqrt{{n}}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\sqrt{{k}}\right]=\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\sqrt{\frac{{k}}{{n}}}=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by SANOGO last updated on 04/Oct/21

$$\mathrm{merci}\:\mathrm{bien} \\ $$
Answered by mindispower last updated on 04/Oct/21
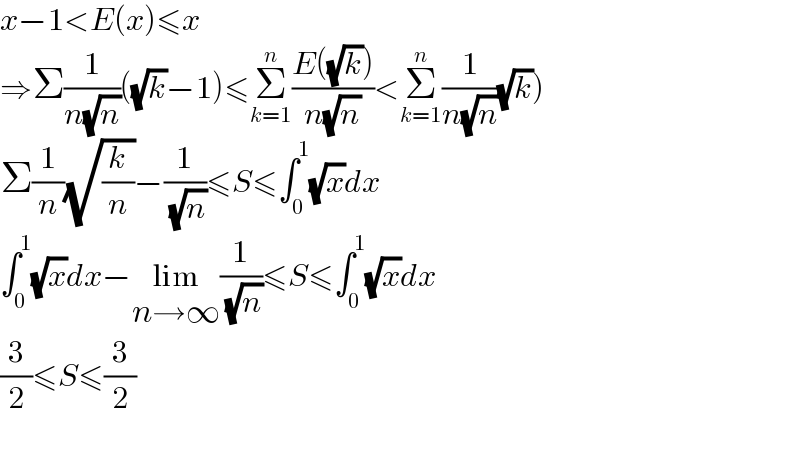
$${x}−\mathrm{1}<{E}\left({x}\right)\leqslant{x} \\ $$$$\left.\Rightarrow\Sigma\frac{\mathrm{1}}{{n}\sqrt{{n}}}\left(\sqrt{{k}}−\mathrm{1}\right)\leqslant\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{E}\left(\sqrt{{k}}\right)}{{n}\sqrt{{n}}}<\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}\sqrt{{n}}}\sqrt{{k}}\right) \\ $$$$\Sigma\frac{\mathrm{1}}{{n}}\sqrt{\frac{{k}}{{n}}}−\frac{\mathrm{1}}{\:\sqrt{{n}}}\leqslant{S}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}{dx}−\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{{n}}}\leqslant{S}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}{dx} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\leqslant{S}\leqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by SANOGO last updated on 04/Oct/21

$${merci}\:{bien} \\ $$
