lim-x-pi-2-2tan-2-x-3-2tan-2-x-10-cot-x-

Question Number 163966 by bobhans last updated on 12/Jan/22

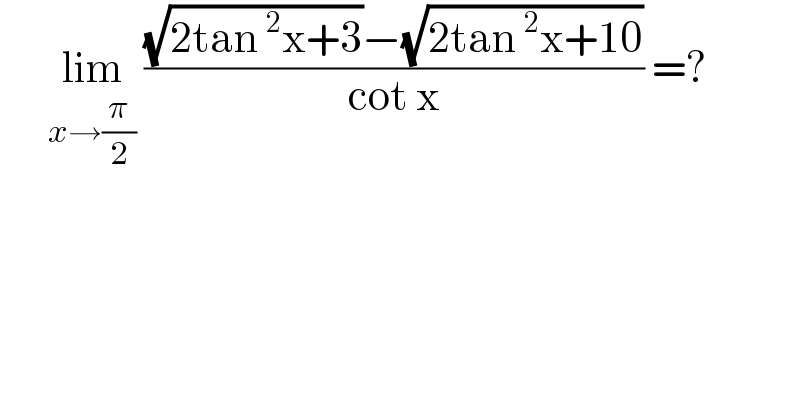
lim_(x→(π/2)) (((√(2tan^2 x+3))−(√(2tan^2 x+10)))/(cot x)) =?

$$\:\:\:\:\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{3}}−\sqrt{\mathrm{2tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{10}}}{\mathrm{cot}\:\mathrm{x}}\:=? \\ $$

Answered by cortano1 last updated on 12/Jan/22

set x=(π/2)+h⇒ { ((tan x=−cot h)),((cot x=−tan h)) :} lim_(h→0) (((√(2cot^2 h+3))−(√(2cot^2 h+10)))/(−tan h)) = lim_(h→0) (((√(2+3tan^2 h))−(√(2+10tan^2 h)))/(−tan^2 h)) = (√2) ×lim_(h→0) (((√(1+((3tan^2 h)/2)))−(√(1+5tan^2 h)))/(−tan^2 h)) =−(√2) ×lim_(h→0) ((((3/4)−(5/2))tan^2 h)/(tan^2 h)) =−(√2) ×(−(7/4))=((7(√2))/4)

$$\:{set}\:{x}=\frac{\pi}{\mathrm{2}}+{h}\Rightarrow\begin{cases}{\mathrm{tan}\:{x}=−\mathrm{cot}\:{h}}\\{\mathrm{cot}\:{x}=−\mathrm{tan}\:{h}}\end{cases} \\ $$$$\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2cot}\:^{\mathrm{2}} {h}+\mathrm{3}}−\sqrt{\mathrm{2cot}\:^{\mathrm{2}} {h}+\mathrm{10}}}{−\mathrm{tan}\:{h}} \\ $$$$\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}+\mathrm{3tan}\:^{\mathrm{2}} {h}}−\sqrt{\mathrm{2}+\mathrm{10tan}\:^{\mathrm{2}} {h}}}{−\mathrm{tan}\:^{\mathrm{2}} {h}} \\ $$$$\:=\:\sqrt{\mathrm{2}}\:×\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+\frac{\mathrm{3tan}\:^{\mathrm{2}} {h}}{\mathrm{2}}}−\sqrt{\mathrm{1}+\mathrm{5tan}\:^{\mathrm{2}} {h}}}{−\mathrm{tan}\:^{\mathrm{2}} {h}} \\ $$$$\:=−\sqrt{\mathrm{2}}\:×\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{5}}{\mathrm{2}}\right)\mathrm{tan}\:^{\mathrm{2}} {h}}{\mathrm{tan}\:^{\mathrm{2}} {h}} \\ $$$$\:=−\sqrt{\mathrm{2}}\:×\left(−\frac{\mathrm{7}}{\mathrm{4}}\right)=\frac{\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$

Facebook Tweet Pin

lim-x-pi-2-2tan-2-x-3-2tan-2-x-10-cot-x-

Leave a Reply Cancel reply