Question Number 161319 by cortano last updated on 16/Dec/21
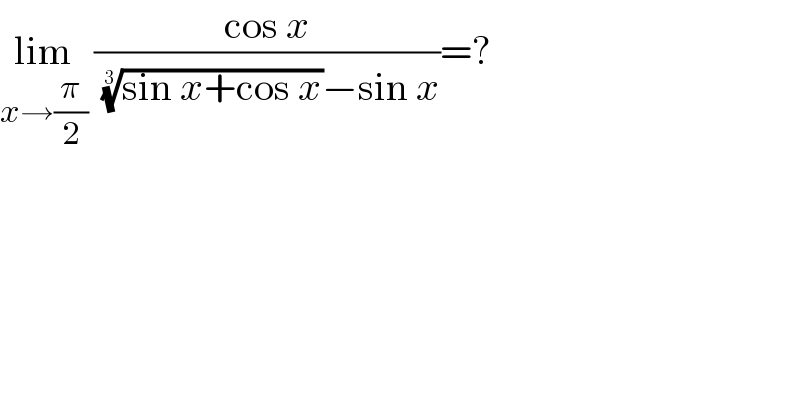
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}}{\:\sqrt[{\mathrm{3}}]{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}−\mathrm{sin}\:{x}}=? \\ $$
Answered by som(math1967) last updated on 16/Dec/21
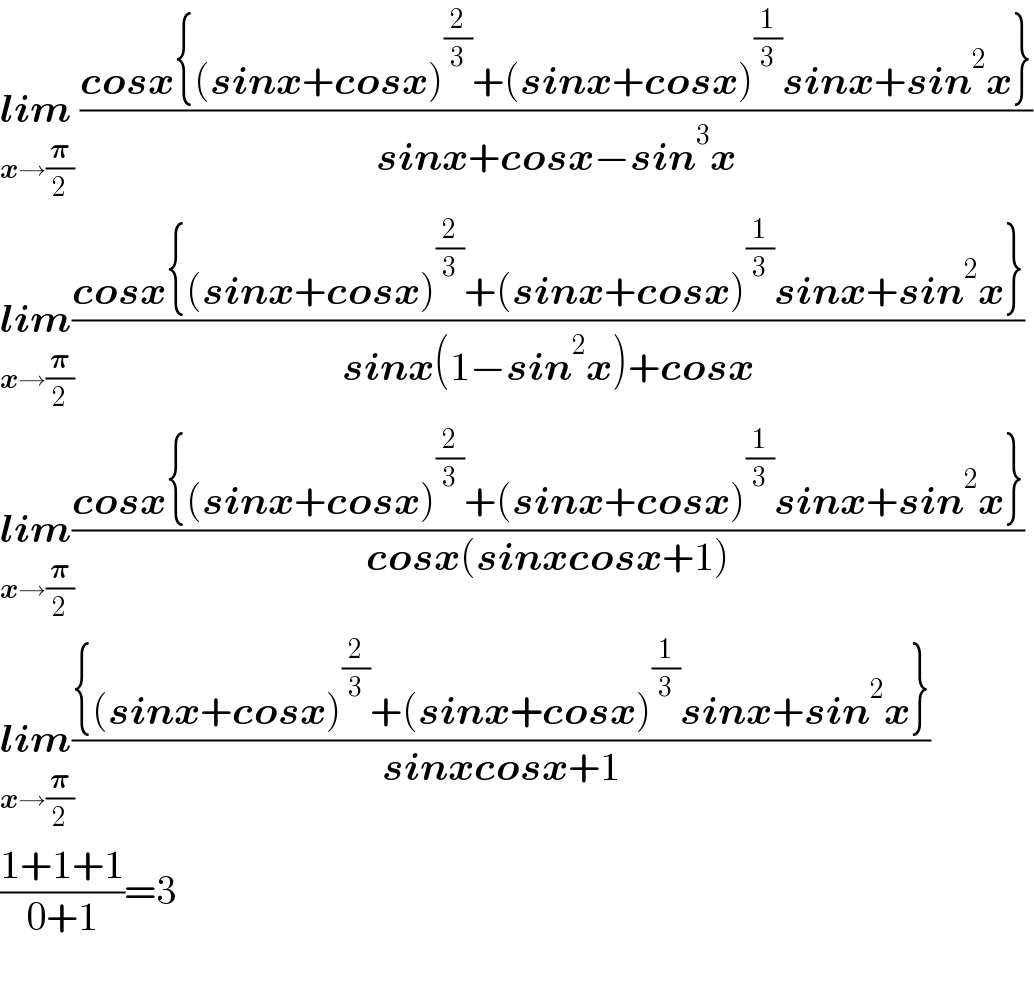
$$\underset{\boldsymbol{{x}}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\boldsymbol{{lim}}}\:\frac{\boldsymbol{{cosx}}\left\{\left(\boldsymbol{{sinx}}+\boldsymbol{{cosx}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} +\left(\boldsymbol{{sinx}}+\boldsymbol{{cosx}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \boldsymbol{{sinx}}+\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{x}}\right\}}{\boldsymbol{{sinx}}+\boldsymbol{{cosx}}−\boldsymbol{{sin}}^{\mathrm{3}} \boldsymbol{{x}}} \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\boldsymbol{{lim}}}\frac{\boldsymbol{{cosx}}\left\{\left(\boldsymbol{{sinx}}+\boldsymbol{{cosx}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} +\left(\boldsymbol{{sinx}}+\boldsymbol{{cosx}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \boldsymbol{{sinx}}+\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{x}}\right\}}{\boldsymbol{{sinx}}\left(\mathrm{1}−\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{x}}\right)+\boldsymbol{{cosx}}} \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\boldsymbol{{lim}}}\frac{\boldsymbol{{cosx}}\left\{\left(\boldsymbol{{sinx}}+\boldsymbol{{cosx}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} +\left(\boldsymbol{{sinx}}+\boldsymbol{{cosx}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \boldsymbol{{sinx}}+\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{x}}\right\}}{\boldsymbol{{cosx}}\left(\boldsymbol{{sinxcosx}}+\mathrm{1}\right)} \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\boldsymbol{{lim}}}\frac{\left\{\left(\boldsymbol{{sinx}}+\boldsymbol{{cosx}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} +\left(\boldsymbol{{sinx}}+\boldsymbol{{cosx}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \boldsymbol{{sinx}}+\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{x}}\right\}}{\boldsymbol{{sinxcosx}}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}+\mathrm{1}+\mathrm{1}}{\mathrm{0}+\mathrm{1}}=\mathrm{3} \\ $$$$ \\ $$
