Question Number 82448 by zainal tanjung last updated on 21/Feb/20
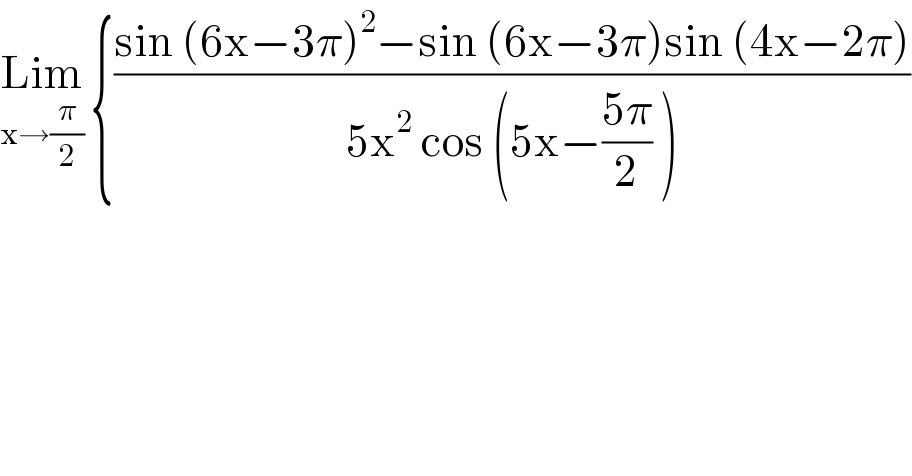
$$\underset{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{Lim}}\:\left\{\frac{\mathrm{sin}\:\left(\mathrm{6x}−\mathrm{3}\pi\right)^{\mathrm{2}} −\mathrm{sin}\:\left(\mathrm{6x}−\mathrm{3}\pi\right)\mathrm{sin}\:\left(\mathrm{4x}−\mathrm{2}\pi\right)}{\mathrm{5x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\mathrm{5x}−\frac{\mathrm{5}\pi}{\mathrm{2}}\:\right)}\right. \\ $$
Commented by jagoll last updated on 21/Feb/20
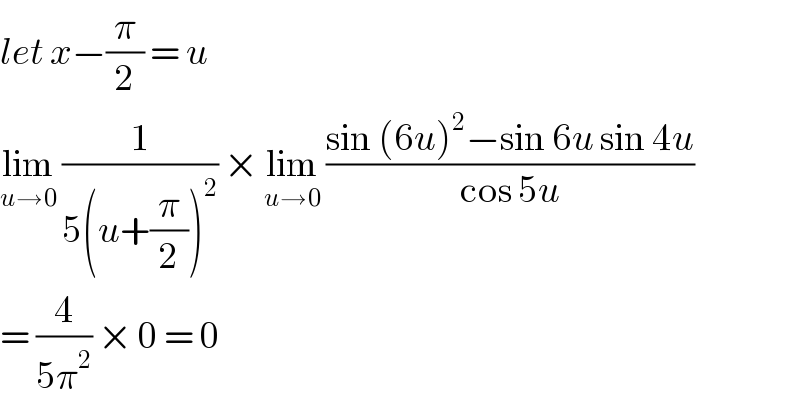
$${let}\:{x}−\frac{\pi}{\mathrm{2}}\:=\:{u} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{5}\left({u}+\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} }\:×\:\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{6}{u}\right)^{\mathrm{2}} −\mathrm{sin}\:\mathrm{6}{u}\:\mathrm{sin}\:\mathrm{4}{u}}{\mathrm{cos}\:\mathrm{5}{u}} \\ $$$$=\:\frac{\mathrm{4}}{\mathrm{5}\pi^{\mathrm{2}} }\:×\:\mathrm{0}\:=\:\mathrm{0} \\ $$
Commented by zainal tanjung last updated on 21/Feb/20
$$\mathrm{You}\:\mathrm{are}\:\mathrm{right}\:\mathrm{sir}….!\:\mathrm{Okey}…. \\ $$
