Question Number 111907 by bemath last updated on 05/Sep/20
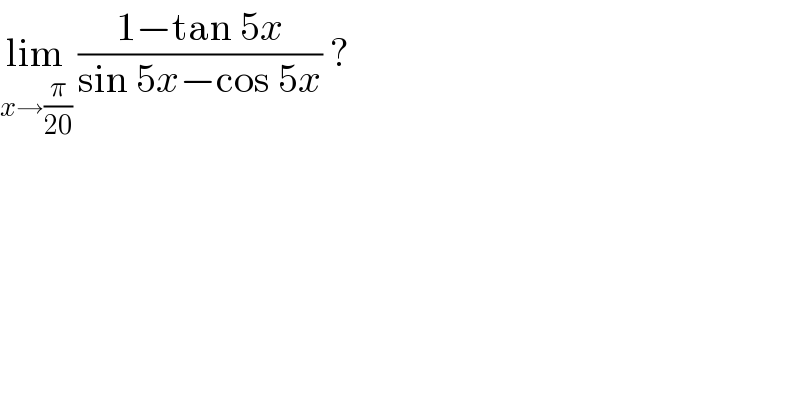
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{20}}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{tan}\:\mathrm{5}{x}}{\mathrm{sin}\:\mathrm{5}{x}−\mathrm{cos}\:\mathrm{5}{x}}\:? \\ $$
Answered by john santu last updated on 05/Sep/20

Answered by john santu last updated on 05/Sep/20
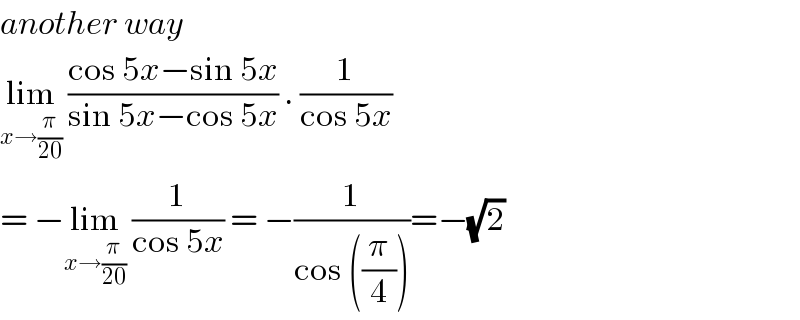
$${another}\:{way}\: \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{20}}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\mathrm{5}{x}−\mathrm{sin}\:\mathrm{5}{x}}{\mathrm{sin}\:\mathrm{5}{x}−\mathrm{cos}\:\mathrm{5}{x}}\:.\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{5}{x}} \\ $$$$=\:−\underset{{x}\rightarrow\frac{\pi}{\mathrm{20}}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{5}{x}}\:=\:−\frac{\mathrm{1}}{\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}\right)}=−\sqrt{\mathrm{2}} \\ $$
