Menu Close

lim-x-pi-4-4-2-cos-x-sin-x-5-cos-x-sin-x-2-

Tinku Tara 0 Comments
Pin




Question Number 119725 by bemath last updated on 26/Oct/20
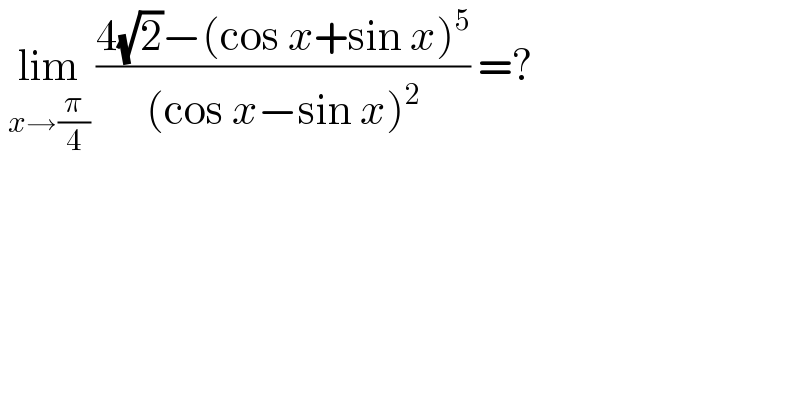
lim_(x→(π/4)) ((4(√2)−(cos x+sin x)^5 )/((cos x−sin x)^2 )) =?
$$\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{4}\sqrt{\mathrm{2}}−\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)^{\mathrm{5}} }{\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)^{\mathrm{2}} }\:=? \\ $$
Commented by bemath last updated on 26/Oct/20
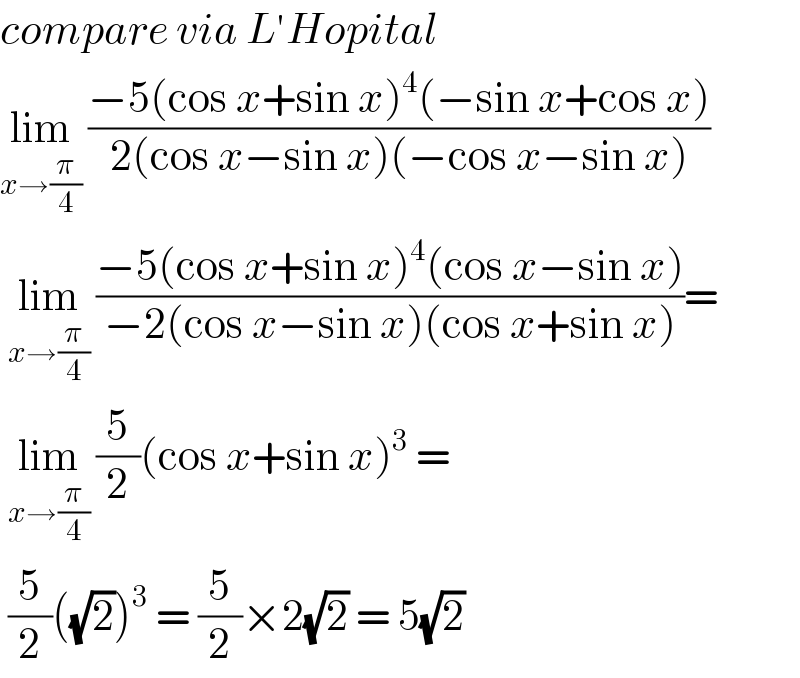
compare via L′Hopital lim_(x→(π/4)) ((−5(cos x+sin x)^4 (−sin x+cos x))/(2(cos x−sin x)(−cos x−sin x))) lim_(x→(π/4)) ((−5(cos x+sin x)^4 (cos x−sin x))/(−2(cos x−sin x)(cos x+sin x)))= lim_(x→(π/4)) (5/2)(cos x+sin x)^3 = (5/2)((√2))^3 = (5/2)×2(√2) = 5(√2)
$${compare}\:{via}\:{L}'{Hopital} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{−\mathrm{5}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)^{\mathrm{4}} \left(−\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)}{\mathrm{2}\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\left(−\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)} \\ $$$$\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{−\mathrm{5}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)^{\mathrm{4}} \left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)}{−\mathrm{2}\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)}= \\ $$$$\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{5}}{\mathrm{2}}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)^{\mathrm{3}} \:= \\ $$$$\:\frac{\mathrm{5}}{\mathrm{2}}\left(\sqrt{\mathrm{2}}\right)^{\mathrm{3}} \:=\:\frac{\mathrm{5}}{\mathrm{2}}×\mathrm{2}\sqrt{\mathrm{2}}\:=\:\mathrm{5}\sqrt{\mathrm{2}}\: \\ $$
Answered by benjo_mathlover last updated on 26/Oct/20
lim_(x→(π/4)) ((4(√2)−4(√2) sin^5 (x+(π/4)))/(1−sin 2x)) = [ let x = (π/4)+z ] lim_(z→0) ((4(√2)(1−sin^5 (z+(π/2))))/(1−sin (2z+(π/2)))) = lim_(z→0) ((4(√2) (1−cos^5 z))/(1−cos 2z)) = lim_(z→0) ((4(√2) (1−(1−(z^2 /2))^5 ))/(1−(1−((4z^2 )/2)))) = lim_(z→0) ((4(√2) (1−(1−((5z^2 )/2))))/(2z^2 )) = lim_(z→0) ((2(√2) (((5z^2 )/2)))/z^2 )= 5(√2)
$$\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{4}\sqrt{\mathrm{2}}\:\mathrm{sin}\:^{\mathrm{5}} \left({x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}}\:= \\ $$$$\left[\:{let}\:{x}\:=\:\frac{\pi}{\mathrm{4}}+{z}\:\right] \\ $$$$\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4}\sqrt{\mathrm{2}}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{5}} \left({z}+\frac{\pi}{\mathrm{2}}\right)\right)}{\mathrm{1}−\mathrm{sin}\:\left(\mathrm{2}{z}+\frac{\pi}{\mathrm{2}}\right)}\:= \\ $$$$\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4}\sqrt{\mathrm{2}}\:\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{5}} {z}\right)}{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{z}}\:=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4}\sqrt{\mathrm{2}}\:\left(\mathrm{1}−\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{5}} \right)}{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{4}{z}^{\mathrm{2}} }{\mathrm{2}}\right)} \\ $$$$=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4}\sqrt{\mathrm{2}}\:\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{5}{z}^{\mathrm{2}} }{\mathrm{2}}\right)\right)}{\mathrm{2}{z}^{\mathrm{2}} }\:=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{5}{z}^{\mathrm{2}} }{\mathrm{2}}\right)}{{z}^{\mathrm{2}} }=\:\mathrm{5}\sqrt{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 26/Oct/20
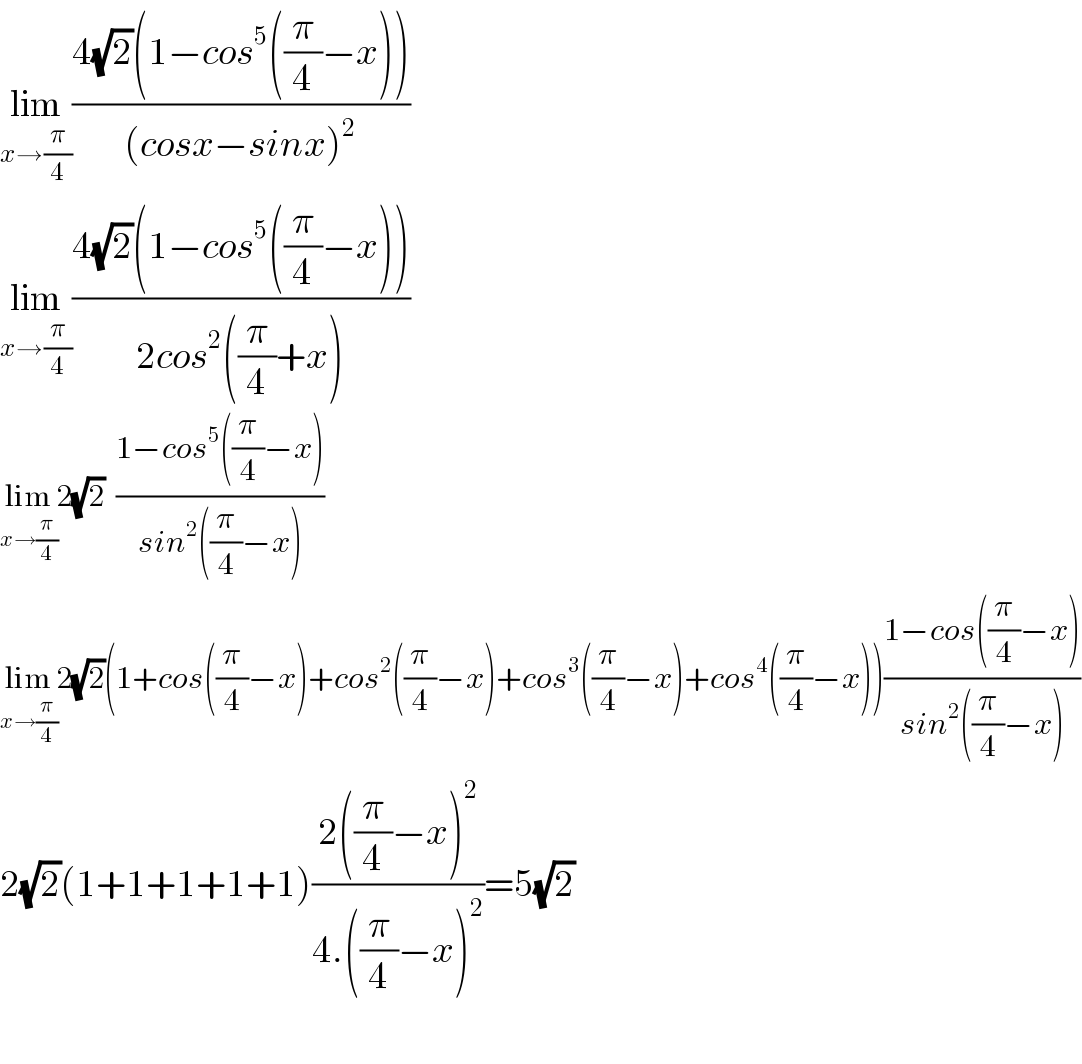
lim_(x→(π/4)) ((4(√2)(1−cos^5 ((π/4)−x)))/((cosx−sinx)^2 )) lim_(x→(π/4)) ((4(√2)(1−cos^5 ((π/4)−x)))/(2cos^2 ((π/4)+x))) lim_(x→(π/4)) 2(√2) ((1−cos^5 ((π/4)−x))/(sin^2 ((π/4)−x))) lim_(x→(π/4)) 2(√2)(1+cos((π/4)−x)+cos^2 ((π/4)−x)+cos^3 ((π/4)−x)+cos^4 ((π/4)−x))((1−cos((π/4)−x))/(sin^2 ((π/4)−x))) 2(√2)(1+1+1+1+1)((2((π/4)−x)^2 )/(4.((π/4)−x)^2 ))=5(√2)
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{\mathrm{4}\sqrt{\mathrm{2}}\left(\mathrm{1}−{cos}^{\mathrm{5}} \left(\frac{\pi}{\mathrm{4}}−{x}\right)\right)}{\left({cosx}−{sinx}\right)^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{\mathrm{4}\sqrt{\mathrm{2}}\left(\mathrm{1}−{cos}^{\mathrm{5}} \left(\frac{\pi}{\mathrm{4}}−{x}\right)\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}+{x}\right)} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}2}\sqrt{\mathrm{2}}\:\:\frac{\mathrm{1}−{cos}^{\mathrm{5}} \left(\frac{\pi}{\mathrm{4}}−{x}\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−{x}\right)} \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}2}\sqrt{\mathrm{2}}\left(\mathrm{1}+{cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)+{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−{x}\right)+{cos}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{4}}−{x}\right)+{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{4}}−{x}\right)\right)\frac{\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−{x}\right)} \\ $$$$\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}\right)\frac{\mathrm{2}\left(\frac{\pi}{\mathrm{4}}−{x}\right)^{\mathrm{2}} }{\mathrm{4}.\left(\frac{\pi}{\mathrm{4}}−{x}\right)^{\mathrm{2}} }=\mathrm{5}\sqrt{\mathrm{2}} \\ $$$$ \\ $$
Answered by Bird last updated on 26/Oct/20
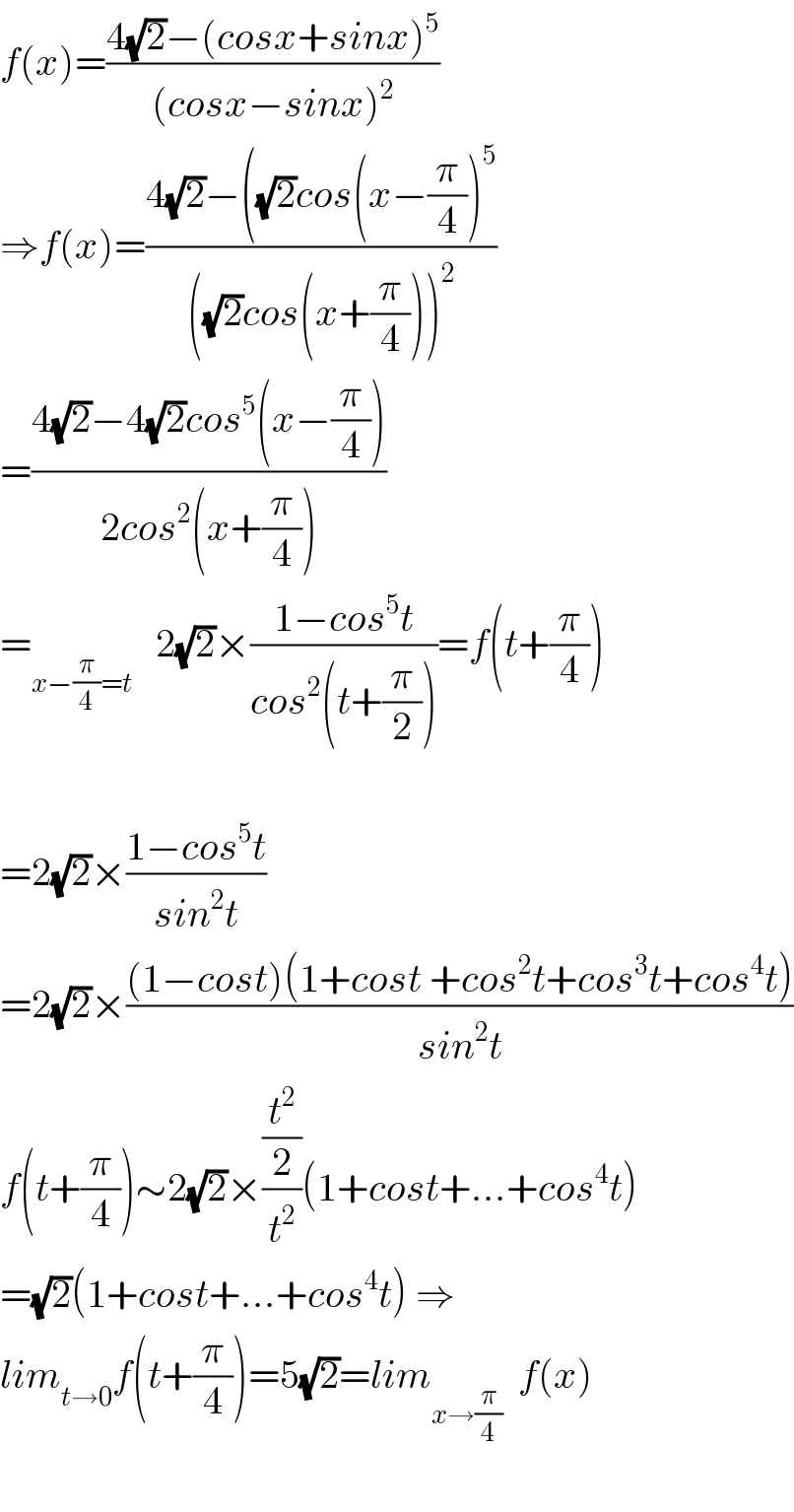
f(x)=((4(√2)−(cosx+sinx)^5 )/((cosx−sinx)^2 )) ⇒f(x)=((4(√2)−((√2)cos(x−(π/4))^5 )/(((√2)cos(x+(π/4)))^2 )) =((4(√2)−4(√2)cos^5 (x−(π/4)))/(2cos^2 (x+(π/4)))) =_(x−(π/4)=t) 2(√2)×((1−cos^5 t)/(cos^2 (t+(π/2))))=f(t+(π/4)) =2(√2)×((1−cos^5 t)/(sin^2 t)) =2(√2)×(((1−cost)(1+cost +cos^2 t+cos^3 t+cos^4 t))/(sin^2 t)) f(t+(π/4))∼2(√2)×((t^2 /2)/t^2 )(1+cost+...+cos^4 t) =(√2)(1+cost+...+cos^4 t) ⇒ lim_(t→0) f(t+(π/4))=5(√2)=lim_(x→(π/4)) f(x)
$${f}\left({x}\right)=\frac{\mathrm{4}\sqrt{\mathrm{2}}−\left({cosx}+{sinx}\right)^{\mathrm{5}} }{\left({cosx}−{sinx}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{4}\sqrt{\mathrm{2}}−\left(\sqrt{\mathrm{2}}{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)^{\mathrm{5}} \right.}{\left(\sqrt{\mathrm{2}}{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right)\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{4}\sqrt{\mathrm{2}}{cos}^{\mathrm{5}} \left({x}−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left({x}+\frac{\pi}{\mathrm{4}}\right)} \\ $$$$=_{{x}−\frac{\pi}{\mathrm{4}}={t}} \:\:\:\mathrm{2}\sqrt{\mathrm{2}}×\frac{\mathrm{1}−{cos}^{\mathrm{5}} {t}}{{cos}^{\mathrm{2}} \left({t}+\frac{\pi}{\mathrm{2}}\right)}={f}\left({t}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$ \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}×\frac{\mathrm{1}−{cos}^{\mathrm{5}} {t}}{{sin}^{\mathrm{2}} {t}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}×\frac{\left(\mathrm{1}−{cost}\right)\left(\mathrm{1}+{cost}\:+{cos}^{\mathrm{2}} {t}+{cos}^{\mathrm{3}} {t}+{cos}^{\mathrm{4}} {t}\right)}{{sin}^{\mathrm{2}} {t}} \\ $$$${f}\left({t}+\frac{\pi}{\mathrm{4}}\right)\sim\mathrm{2}\sqrt{\mathrm{2}}×\frac{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}}{{t}^{\mathrm{2}} }\left(\mathrm{1}+{cost}+…+{cos}^{\mathrm{4}} {t}\right) \\ $$$$=\sqrt{\mathrm{2}}\left(\mathrm{1}+{cost}+…+{cos}^{\mathrm{4}} {t}\right)\:\Rightarrow \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} {f}\left({t}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{5}\sqrt{\mathrm{2}}={lim}_{{x}\rightarrow\frac{\pi}{\mathrm{4}}} \:\:{f}\left({x}\right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *