Menu Close

lim-x-pi-4-sin-x-cos-x-2-tan-x-sin-x-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 105126 by bemath last updated on 26/Jul/20
lim_(x→(π/4)) ((sin x+cos x−(√2)tan x)/(sin x−cos x))
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}−\sqrt{\mathrm{2}}\mathrm{tan}\:{x}}{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Jul/20
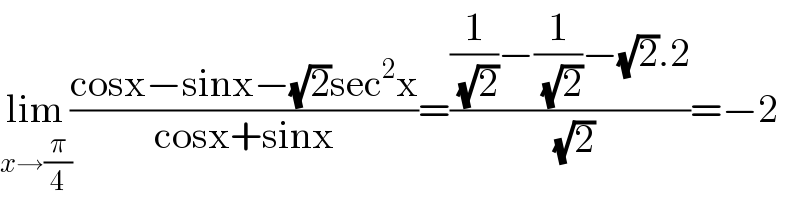
lim_(x→(π/4)) ((cosx−sinx−(√2)sec^2 x)/(cosx+sinx))=(((1/( (√2)))−(1/( (√2)))−(√2).2)/( (√2)))=−2
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{\mathrm{cosx}−\mathrm{sinx}−\sqrt{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\mathrm{cosx}+\mathrm{sinx}}=\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\sqrt{\mathrm{2}}.\mathrm{2}}{\:\sqrt{\mathrm{2}}}=−\mathrm{2} \\ $$
Answered by bramlex last updated on 26/Jul/20
sin x+cos x = (√2) sin (x+(π/4)) sin x−cos x = (√2) sin (x−(π/4)) set x = w+(π/4) lim_(w→0) (((√2) sin (w+(π/2))−(√2) tan (w+(π/4)))/( (√2) sin (w))) lim_(w→0) ((cos w−{((1+tan w)/(1−tan w))})/(sin w)) lim_(w→0) ((cos w−sin w−1−tan w)/(sin w(1−tan w))) lim_(x→0) (((cos w−1)−sin w−tan w)/(sin w(1−tan w))) lim_(w→0) ((((1−(w^2 /2))−1)−(w−(w^3 /6))−(w+(w^3 /3)))/((w−(w^3 /6))(1−(w+(w^3 /3))))) lim_(w→0) ((−(w^2 /2)−2w−(w^3 /6))/((w−(w^3 /6))(1−w−(w^3 /3)))) = −2
$$\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\:=\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\:\left({x}+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\:=\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\:\left({x}−\frac{\pi}{\mathrm{4}}\right) \\ $$$${set}\:{x}\:=\:{w}+\frac{\pi}{\mathrm{4}} \\ $$$$\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left({w}+\frac{\pi}{\mathrm{2}}\right)−\sqrt{\mathrm{2}}\:\mathrm{tan}\:\left({w}+\frac{\pi}{\mathrm{4}}\right)}{\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left({w}\right)} \\ $$$$\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{w}−\left\{\frac{\mathrm{1}+\mathrm{tan}\:{w}}{\mathrm{1}−\mathrm{tan}\:{w}}\right\}}{\mathrm{sin}\:{w}} \\ $$$$\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:{w}−\mathrm{sin}\:{w}−\mathrm{1}−\mathrm{tan}\:{w}}{\mathrm{sin}\:{w}\left(\mathrm{1}−\mathrm{tan}\:{w}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{cos}\:{w}−\mathrm{1}\right)−\mathrm{sin}\:{w}−\mathrm{tan}\:{w}}{\mathrm{sin}\:{w}\left(\mathrm{1}−\mathrm{tan}\:{w}\right)} \\ $$$$\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\left(\mathrm{1}−\frac{{w}^{\mathrm{2}} }{\mathrm{2}}\right)−\mathrm{1}\right)−\left({w}−\frac{{w}^{\mathrm{3}} }{\mathrm{6}}\right)−\left({w}+\frac{{w}^{\mathrm{3}} }{\mathrm{3}}\right)}{\left({w}−\frac{{w}^{\mathrm{3}} }{\mathrm{6}}\right)\left(\mathrm{1}−\left({w}+\frac{{w}^{\mathrm{3}} }{\mathrm{3}}\right)\right)} \\ $$$$\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\frac{{w}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{w}−\frac{{w}^{\mathrm{3}} }{\mathrm{6}}}{\left({w}−\frac{{w}^{\mathrm{3}} }{\mathrm{6}}\right)\left(\mathrm{1}−{w}−\frac{{w}^{\mathrm{3}} }{\mathrm{3}}\right)}\:=\:−\mathrm{2}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *