Question Number 175362 by cortano1 last updated on 28/Aug/22
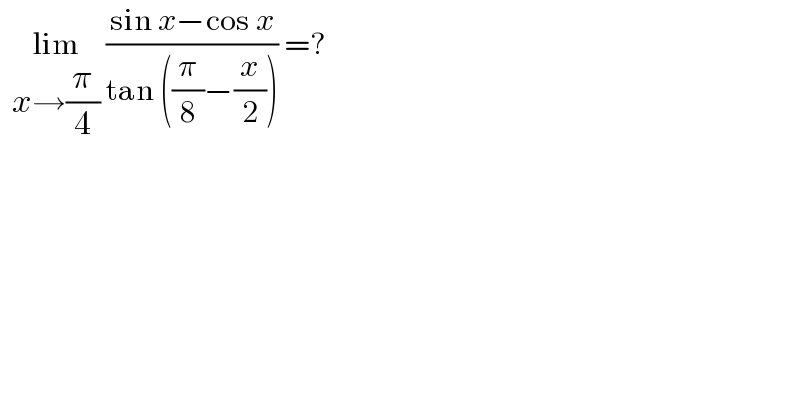
$$\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{8}}−\frac{{x}}{\mathrm{2}}\right)}\:=? \\ $$
Commented by infinityaction last updated on 28/Aug/22
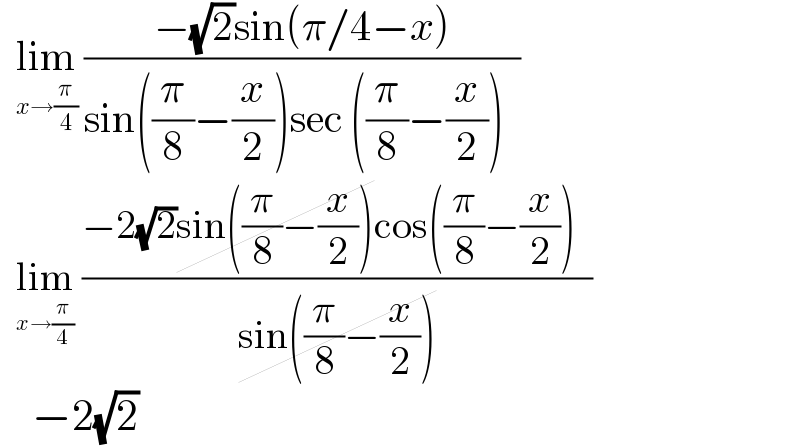
$$\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{−\sqrt{\mathrm{2}}\mathrm{sin}\left(\pi/\mathrm{4}−{x}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{8}}−\frac{{x}}{\mathrm{2}}\right)\mathrm{sec}\:\left(\frac{\pi}{\mathrm{8}}−\frac{{x}}{\mathrm{2}}\right)\:\:} \\ $$$$\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{−\mathrm{2}\sqrt{\mathrm{2}}\cancel{\mathrm{sin}\left(\frac{\pi}{\mathrm{8}}−\frac{{x}}{\mathrm{2}}\right)}\mathrm{cos}\left(\frac{\pi}{\mathrm{8}}−\frac{{x}}{\mathrm{2}}\right)\:\:}{\cancel{\mathrm{sin}\left(\frac{\pi}{\mathrm{8}}−\frac{{x}}{\mathrm{2}}\right)}} \\ $$$$\:\:\:\:−\mathrm{2}\sqrt{\mathrm{2}} \\ $$
Commented by CElcedricjunior last updated on 28/Aug/22
![lim_(x→(𝛑/4)) ((sinx−cosx)/(tan((𝛑/8)−(x/2))))=(0/0)=FI end apply hospital lim_(x→(𝛑/4)) ((cosx+sinx)/(−(1/2)[1+tan^2 ((𝛑/8)−(x/2))]))=((√2)/(−(1/2))) lim_(x→(𝛑/4)) ((sinx−cosx)/(tan((𝛑/8)−(x/2))))=−2(√2) .........le ce^� le^� bre cedric junior.........](https://www.tinkutara.com/question/Q175366.png)
$$\underset{{x}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{4}}} {\mathrm{lim}}\frac{\boldsymbol{{sinx}}−\boldsymbol{{cosx}}}{\boldsymbol{{tan}}\left(\frac{\boldsymbol{\pi}}{\mathrm{8}}−\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)}=\frac{\mathrm{0}}{\mathrm{0}}={F}\boldsymbol{{I}} \\ $$$$\boldsymbol{{end}}\:\boldsymbol{{apply}}\:\boldsymbol{{hospital}}\: \\ $$$$\underset{{x}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{4}}} {\mathrm{lim}}\frac{\boldsymbol{{cosx}}+\boldsymbol{{sinx}}}{−\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}}}\left(\frac{\boldsymbol{\pi}}{\mathrm{8}}−\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)\right]}=\frac{\sqrt{\mathrm{2}}}{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\underset{{x}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{4}}} {\mathrm{lim}}\frac{\boldsymbol{{sinx}}−\boldsymbol{{cosx}}}{\boldsymbol{{tan}}\left(\frac{\boldsymbol{\pi}}{\mathrm{8}}−\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)}=−\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\: \\ $$$$………\boldsymbol{{le}}\:{c}\acute {{e}l}\grave {{e}bre}\:{cedric}\:{junior}……… \\ $$
Answered by BaliramKumar last updated on 28/Aug/22
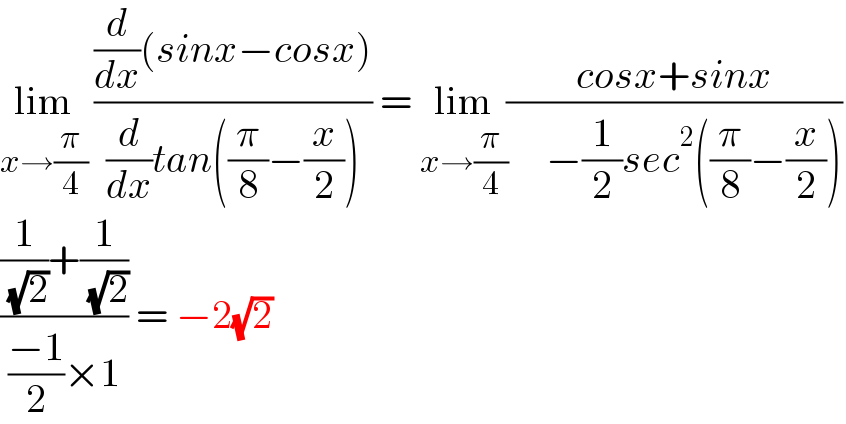
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left({sinx}−{cosx}\right)}{\frac{{d}}{{dx}}{tan}\left(\frac{\pi}{\mathrm{8}}−\frac{{x}}{\mathrm{2}}\right)}\:=\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\frac{{cosx}+{sinx}}{\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}−\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\frac{−\mathrm{1}}{\mathrm{2}}×\mathrm{1}}\:=\:−\mathrm{2}\sqrt{\mathrm{2}} \\ $$
