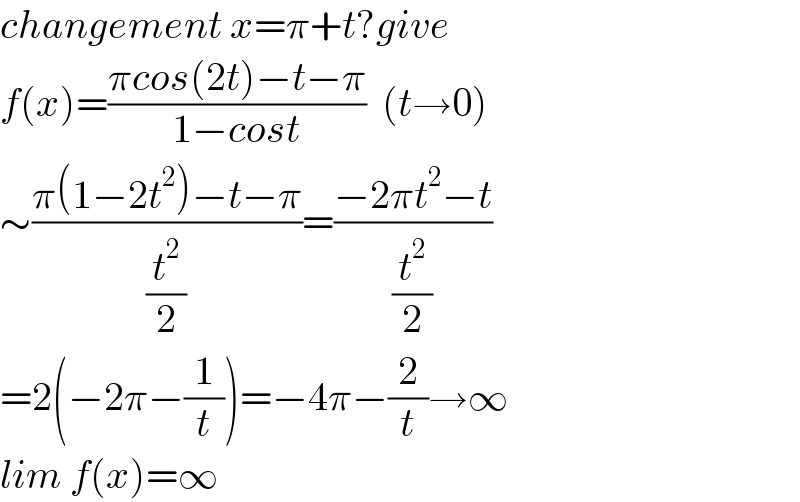lim-x-pi-picos2x-x-1-cosx-

Question Number 169182 by mathlove last updated on 25/Apr/22

\lim_{x \to π} \frac{π c o s 2 x - x}{1 + c o s x} = ?

Commented by infinityaction last updated on 25/Apr/22

u s e l h o s p i t a l r u l e

p = \lim_{x \to π} \frac{- 2 π \sin 2 x - 1}{- \sin x}

p = \lim_{x \to π} \frac{2 π \sin 2 x + 1}{\sin x}

p = \frac{2 π \times 0 + 1}{0} = \frac{1}{0}

p = \infty

Answered by qaz last updated on 25/Apr/22

\lim_{x \to π} \frac{π \cos 2 x - x}{1 + \cos x} = \lim_{x \to 0} \frac{π \cos 2 x - x - π}{1 - \cos x} = \lim_{x \to 0} \frac{π (1 - {2 x}^{2}) - x - π}{\frac{1}{2} x^{2}} = \pm \infty

Commented by JDamian last updated on 25/Apr/22

wrong

Commented by qaz last updated on 25/Apr/22

why would you default to^{'} x \to π^{+}^{'} ? why not^{'} x \to π^{-}^{'} ?

Answered by Mathspace last updated on 25/Apr/22

c h a n g e m e n t x = π + t ? g i v e

f (x) = \frac{π c o s (2 t) - t - π}{1 - c o s t} (t \to 0)

\sim \frac{π (1 - 2 t^{2}) - t - π}{\frac{t^{2}}{2}} = \frac{- 2 π t^{2} - t}{\frac{t^{2}}{2}}

= 2 (- 2 π - \frac{1}{t}) = - 4 π - \frac{2}{t} \to \infty

l i m f (x) = \infty