Menu Close

lim-x-pi-tan-x-1-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 160609 by cortano last updated on 03/Dec/21
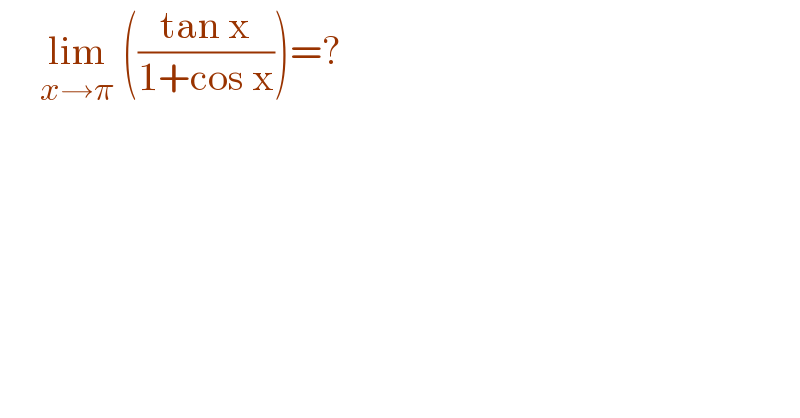
lim_(x→π) (((tan x)/(1+cos x)))=?
$$\:\:\:\:\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\left(\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\right)=? \\ $$
Answered by Ar Brandon last updated on 03/Dec/21
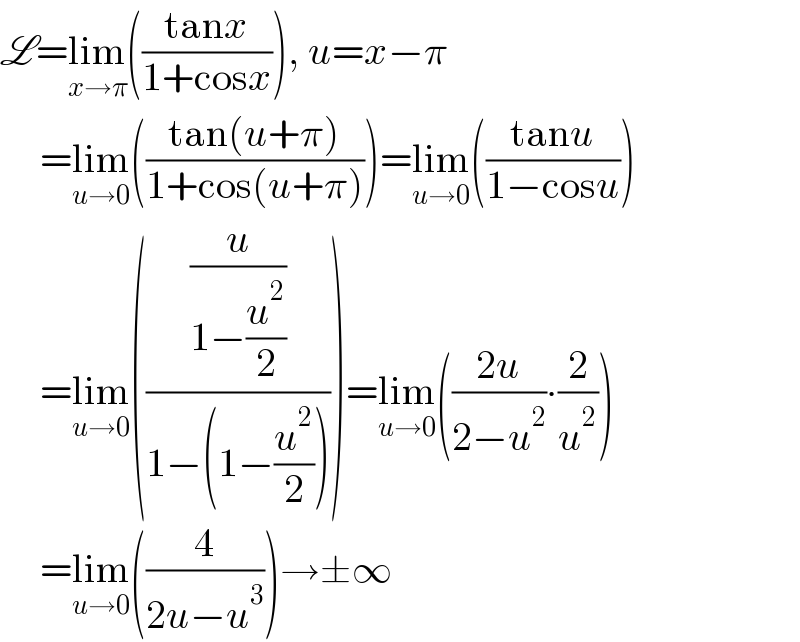
L=lim_(x→π) (((tanx)/(1+cosx))), u=x−π =lim_(u→0) (((tan(u+π))/(1+cos(u+π))))=lim_(u→0) (((tanu)/(1−cosu))) =lim_(u→0) (((u/(1−(u^2 /2)))/(1−(1−(u^2 /2)))))=lim_(u→0) (((2u)/(2−u^2 ))∙(2/u^2 )) =lim_(u→0) ((4/(2u−u^3 )))→±∞
$$\mathscr{L}=\underset{{x}\rightarrow\pi} {\mathrm{lim}}\left(\frac{\mathrm{tan}{x}}{\mathrm{1}+\mathrm{cos}{x}}\right),\:{u}={x}−\pi \\ $$$$\:\:\:\:\:=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{tan}\left({u}+\pi\right)}{\mathrm{1}+\mathrm{cos}\left({u}+\pi\right)}\right)=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{tan}{u}}{\mathrm{1}−\mathrm{cos}{u}}\right) \\ $$$$\:\:\:\:\:=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\frac{{u}}{\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}}}{\mathrm{1}−\left(\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right)}\right)=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}{u}}{\mathrm{2}−{u}^{\mathrm{2}} }\centerdot\frac{\mathrm{2}}{{u}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{4}}{\mathrm{2}{u}−{u}^{\mathrm{3}} }\right)\rightarrow\pm\infty \\ $$
Answered by alephzero last updated on 03/Dec/21
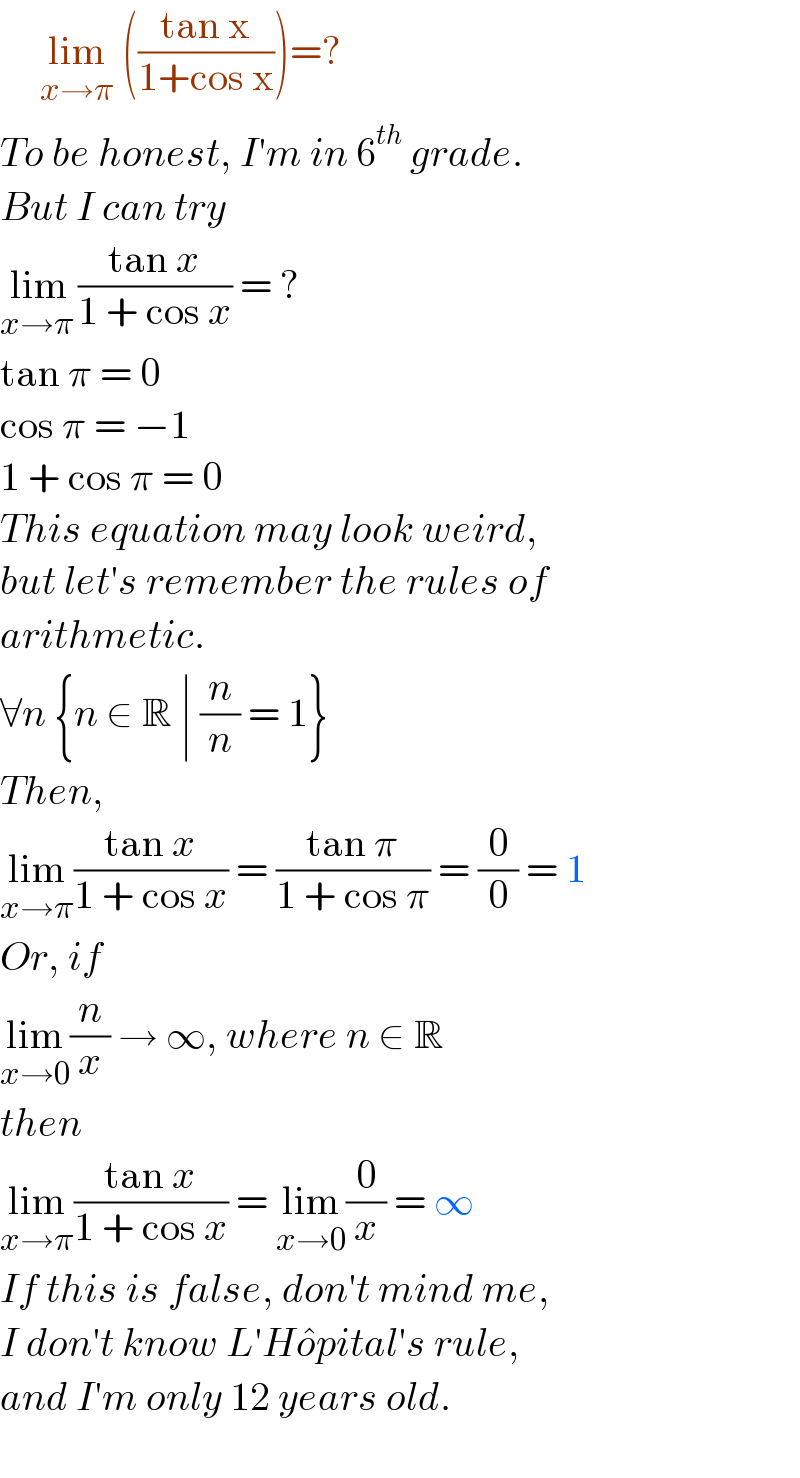
lim_(x→π) (((tan x)/(1+cos x)))=? To be honest, I′m in 6^(th) grade. But I can try lim_(x→π ) ((tan x)/(1 + cos x)) = ? tan π = 0 cos π = −1 1 + cos π = 0 This equation may look weird, but let′s remember the rules of arithmetic. ∀n {n ∈ R ∣ (n/n) = 1} Then, lim_(x→π) ((tan x)/(1 + cos x)) = ((tan π)/(1 + cos π)) = (0/0) = 1 Or, if lim_(x→0) (n/x) → ∞, where n ∈ R then lim_(x→π) ((tan x)/(1 + cos x)) = lim_(x→0) (0/x) = ∞ If this is false, don′t mind me, I don′t know L′Ho^� pital′s rule, and I′m only 12 years old.
$$\:\:\:\:\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\left(\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\right)=? \\ $$$${To}\:{be}\:{honest},\:{I}'{m}\:{in}\:\mathrm{6}^{{th}} \:{grade}. \\ $$$${But}\:{I}\:{can}\:{try} \\ $$$$\underset{{x}\rightarrow\pi\:} {\mathrm{lim}}\frac{\mathrm{tan}\:{x}}{\mathrm{1}\:+\:\mathrm{cos}\:{x}}\:=\:? \\ $$$$\mathrm{tan}\:\pi\:=\:\mathrm{0} \\ $$$$\mathrm{cos}\:\pi\:=\:−\mathrm{1} \\ $$$$\mathrm{1}\:+\:\mathrm{cos}\:\pi\:=\:\mathrm{0} \\ $$$${This}\:{equation}\:{may}\:{look}\:{weird}, \\ $$$${but}\:{let}'{s}\:{remember}\:{the}\:{rules}\:{of} \\ $$$${arithmetic}. \\ $$$$\forall{n}\:\left\{{n}\:\in\:\mathbb{R}\:\mid\:\frac{{n}}{{n}}\:=\:\mathrm{1}\right\} \\ $$$${Then}, \\ $$$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{\mathrm{tan}\:{x}}{\mathrm{1}\:+\:\mathrm{cos}\:{x}}\:=\:\frac{\mathrm{tan}\:\pi}{\mathrm{1}\:+\:\mathrm{cos}\:\pi}\:=\:\frac{\mathrm{0}}{\mathrm{0}}\:=\:\mathrm{1} \\ $$$${Or},\:{if} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{n}}{{x}}\:\rightarrow\:\infty,\:{where}\:{n}\:\in\:\mathbb{R} \\ $$$${then} \\ $$$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{\mathrm{tan}\:{x}}{\mathrm{1}\:+\:\mathrm{cos}\:{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{0}}{{x}}\:=\:\infty \\ $$$${If}\:{this}\:{is}\:{false},\:{don}'{t}\:{mind}\:{me}, \\ $$$${I}\:{don}'{t}\:{know}\:{L}'{H}\hat {{o}pital}'{s}\:{rule}, \\ $$$${and}\:{I}'{m}\:{only}\:\mathrm{12}\:{years}\:{old}. \\ $$$$ \\ $$
Answered by tounghoungko last updated on 03/Dec/21
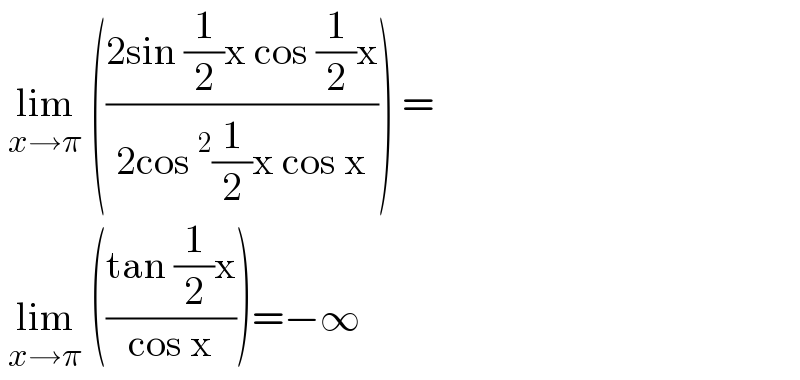
lim_(x→π) (((2sin (1/2)x cos (1/2)x)/(2cos^2 (1/2)x cos x))) = lim_(x→π) (((tan (1/2)x)/(cos x)))=−∞
$$\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\left(\frac{\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}}{\mathrm{2cos}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}\right)\:= \\ $$$$\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\left(\frac{\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}\right)=−\infty \\ $$
Answered by Mathspace last updated on 03/Dec/21
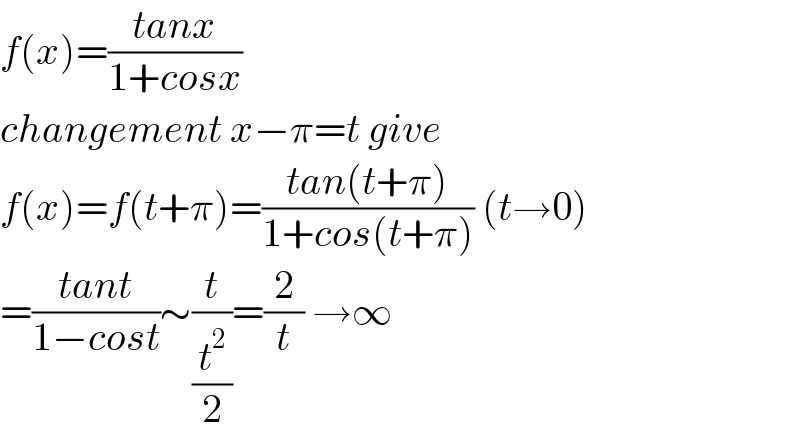
f(x)=((tanx)/(1+cosx)) changement x−π=t give f(x)=f(t+π)=((tan(t+π))/(1+cos(t+π))) (t→0) =((tant)/(1−cost))∼(t/(t^2 /2))=(2/t) →∞
$${f}\left({x}\right)=\frac{{tanx}}{\mathrm{1}+{cosx}} \\ $$$${changement}\:{x}−\pi={t}\:{give} \\ $$$${f}\left({x}\right)={f}\left({t}+\pi\right)=\frac{{tan}\left({t}+\pi\right)}{\mathrm{1}+{cos}\left({t}+\pi\right)}\:\left({t}\rightarrow\mathrm{0}\right) \\ $$$$=\frac{{tant}}{\mathrm{1}−{cost}}\sim\frac{{t}}{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}}=\frac{\mathrm{2}}{{t}}\:\rightarrow\infty \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *