Question Number 163650 by mathlove last updated on 09/Jan/22
$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{{x}^{\pi^{{x}} } −\pi^{{x}^{\pi} } }{{x}−\pi}=? \\ $$
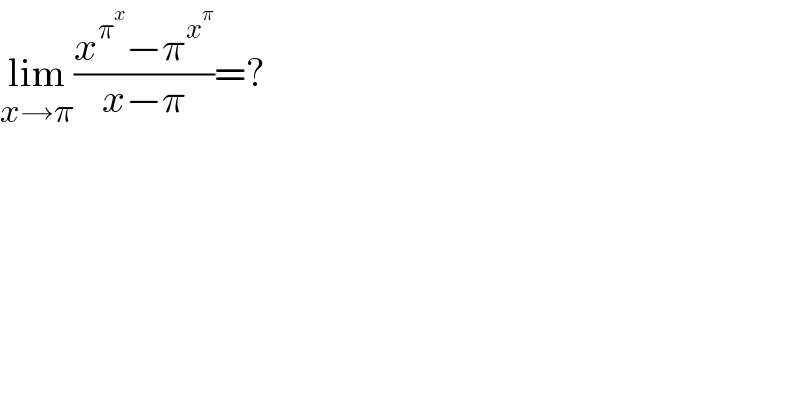
Commented by Zaynal last updated on 09/Jan/22
$$\mathrm{is}'\mathrm{t}\:\mathrm{not}\:\mathrm{value}\:\mathrm{of}\:\mathrm{limit} \\ $$
Commented by mathlove last updated on 09/Jan/22
$${way}? \\ $$
Answered by mr W last updated on 09/Jan/22
![generally: (a^(f(x)) )′=(e^(f(x) ln a) )′=a^(f(x)) (ln a)f′(x) (x^(f(x)) )′=(e^(f(x)ln x) )′=x^(f(x)) (((f(x))/x)+f′(x)ln x) lim_(x→a) ((x^a^x −a^x^a )/(x−a)) =lim_(x→a) (x^a^x −a^x^a )′ =lim_(x→a) {x^a^x ((a^x /x)+(ln x) (a^x )^′ )−a^x^a (ln a)(x^a )′} =lim_(x→a) {x^a^x [(a^x /x)+(ln x) (a^x )(ln a)]−a^x^a a(ln a)(x^(a−1) )} = {a^a^a [a^(a−1) +(ln a)^2 (a^a )]−a^a^a (ln a)(a^a )} = a^(a^a +a−1) {1+a(ln a)^2 −a(ln a)} = a^(a^a +a−1) [a (ln a)(ln a−1) +1] lim_(x→π) ((x^π^x −π^x^π )/(x−π))=π^(π^π +π−1) [π (ln π)(ln π−1) +1]](https://www.tinkutara.com/question/Q163672.png)
$${generally}: \\ $$$$\left({a}^{{f}\left({x}\right)} \right)'=\left({e}^{{f}\left({x}\right)\:{ln}\:{a}} \right)'={a}^{{f}\left({x}\right)} \left({ln}\:{a}\right){f}'\left({x}\right) \\ $$$$\left({x}^{{f}\left({x}\right)} \right)'=\left({e}^{{f}\left({x}\right)\mathrm{ln}\:{x}} \right)'={x}^{{f}\left({x}\right)} \left(\frac{{f}\left({x}\right)}{{x}}+{f}'\left({x}\right)\mathrm{ln}\:{x}\right) \\ $$$$ \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{x}^{{a}^{{x}} } −{a}^{{x}^{{a}} } }{{x}−{a}} \\ $$$$=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\left({x}^{{a}^{{x}} } −{a}^{{x}^{{a}} } \right)' \\ $$$$=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\left\{{x}^{{a}^{{x}} } \left(\frac{{a}^{{x}} }{{x}}+\left(\mathrm{ln}\:{x}\right)\:\left({a}^{{x}} \right)^{'} \right)−{a}^{{x}^{{a}} } \left(\mathrm{ln}\:{a}\right)\left({x}^{{a}} \right)'\right\} \\ $$$$=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\left\{{x}^{{a}^{{x}} } \left[\frac{{a}^{{x}} }{{x}}+\left(\mathrm{ln}\:{x}\right)\:\left({a}^{{x}} \right)\left(\mathrm{ln}\:{a}\right)\right]−{a}^{{x}^{{a}} } {a}\left(\mathrm{ln}\:{a}\right)\left({x}^{{a}−\mathrm{1}} \right)\right\} \\ $$$$=\:\left\{{a}^{{a}^{{a}} } \left[{a}^{{a}−\mathrm{1}} +\left(\mathrm{ln}\:{a}\right)^{\mathrm{2}} \:\left({a}^{{a}} \right)\right]−{a}^{{a}^{{a}} } \left(\mathrm{ln}\:{a}\right)\left({a}^{{a}} \right)\right\} \\ $$$$=\:{a}^{{a}^{{a}} +{a}−\mathrm{1}} \left\{\mathrm{1}+{a}\left(\mathrm{ln}\:{a}\right)^{\mathrm{2}} \:−{a}\left(\mathrm{ln}\:{a}\right)\right\} \\ $$$$=\:{a}^{{a}^{{a}} +{a}−\mathrm{1}} \left[{a}\:\left(\mathrm{ln}\:{a}\right)\left(\mathrm{ln}\:{a}−\mathrm{1}\right)\:+\mathrm{1}\right] \\ $$$$ \\ $$$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{{x}^{\pi^{{x}} } −\pi^{{x}^{\pi} } }{{x}−\pi}=\pi^{\pi^{\pi} +\pi−\mathrm{1}} \left[\pi\:\left(\mathrm{ln}\:\pi\right)\left(\mathrm{ln}\:\pi−\mathrm{1}\right)\:+\mathrm{1}\right] \\ $$
Commented by mathlove last updated on 09/Jan/22
$${thanks}\:\:{mr}\:\:{W} \\ $$
Commented by Tawa11 last updated on 09/Jan/22
$$\mathrm{Great}\:\mathrm{sir} \\ $$