Question Number 171385 by cortano1 last updated on 14/Jun/22
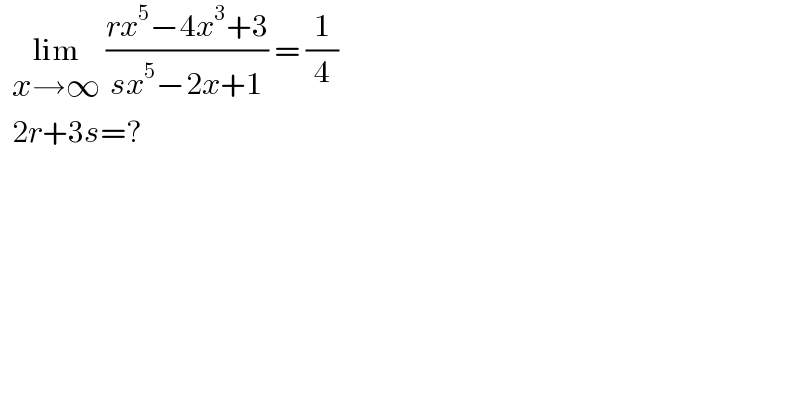
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{rx}^{\mathrm{5}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{3}}{{sx}^{\mathrm{5}} −\mathrm{2}{x}+\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\mathrm{2}{r}+\mathrm{3}{s}=? \\ $$
Answered by qaz last updated on 14/Jun/22

$$\underset{{x}\rightarrow\infty} {{lim}}\frac{{rx}^{\mathrm{5}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{3}}{{sx}^{\mathrm{5}} −\mathrm{2}{x}+\mathrm{1}}=\frac{{r}}{{s}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{2}{r}+\mathrm{3}{s}=\:??? \\ $$
Answered by nurtani last updated on 14/Jun/22

$$\mathrm{14}\:??? \\ $$
Answered by alephzero last updated on 14/Jun/22
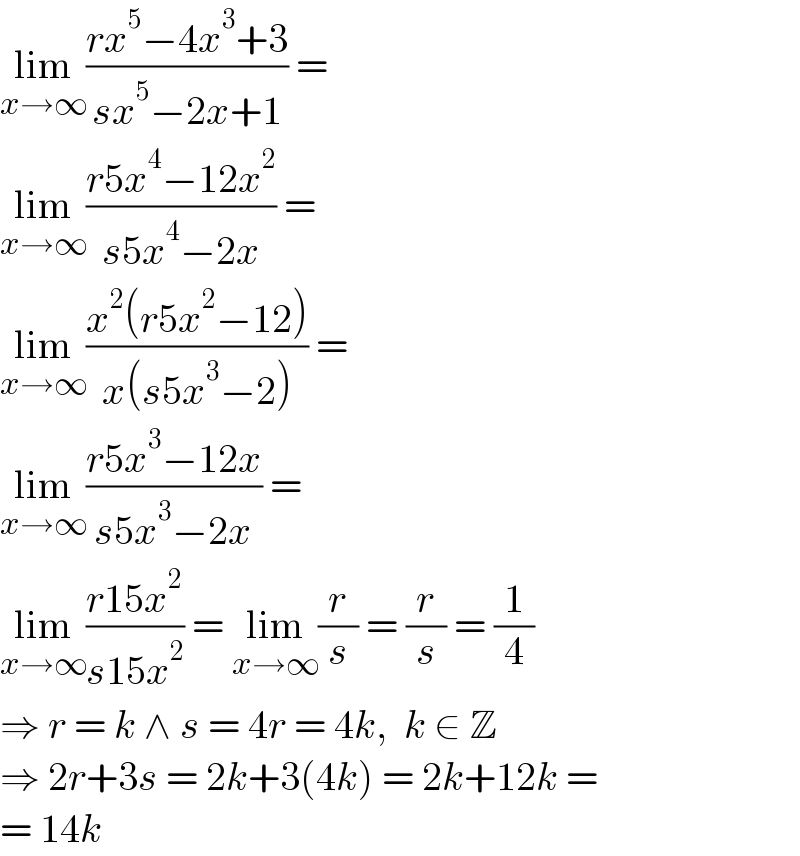
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{rx}^{\mathrm{5}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{3}}{{sx}^{\mathrm{5}} −\mathrm{2}{x}+\mathrm{1}}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{r}\mathrm{5}{x}^{\mathrm{4}} −\mathrm{12}{x}^{\mathrm{2}} }{{s}\mathrm{5}{x}^{\mathrm{4}} −\mathrm{2}{x}}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} \left({r}\mathrm{5}{x}^{\mathrm{2}} −\mathrm{12}\right)}{{x}\left({s}\mathrm{5}{x}^{\mathrm{3}} −\mathrm{2}\right)}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{r}\mathrm{5}{x}^{\mathrm{3}} −\mathrm{12}{x}}{{s}\mathrm{5}{x}^{\mathrm{3}} −\mathrm{2}{x}}\:= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{r}\mathrm{15}{x}^{\mathrm{2}} }{{s}\mathrm{15}{x}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{r}}{{s}}\:=\:\frac{{r}}{{s}}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:{r}\:=\:{k}\:\wedge\:{s}\:=\:\mathrm{4}{r}\:=\:\mathrm{4}{k},\:\:{k}\:\in\:\mathbb{Z} \\ $$$$\Rightarrow\:\mathrm{2}{r}+\mathrm{3}{s}\:=\:\mathrm{2}{k}+\mathrm{3}\left(\mathrm{4}{k}\right)\:=\:\mathrm{2}{k}+\mathrm{12}{k}\:= \\ $$$$=\:\mathrm{14}{k} \\ $$
