Menu Close

lim-x-sin-pi-2n-sin-2pi-2n-sin-3pi-2n-sin-n-1-pi-n-1-n-

Tinku Tara 0 Comments
Pin




Question Number 163658 by mathlove last updated on 09/Jan/22
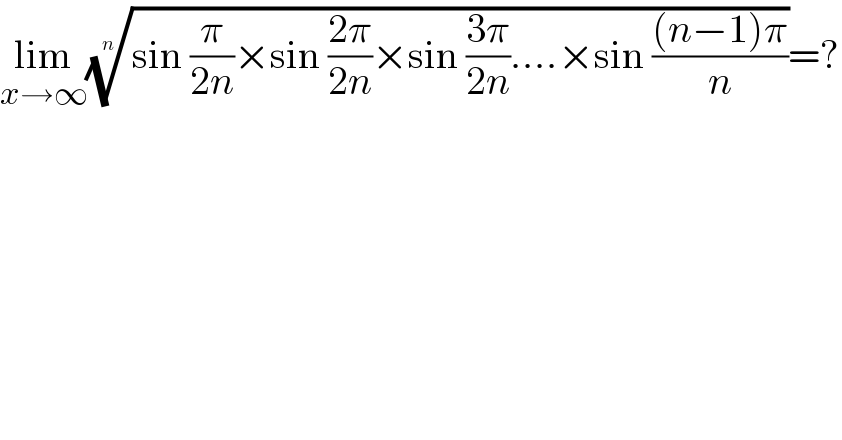
lim_(x→∞) ((sin (π/(2n))×sin ((2π)/(2n))×sin ((3π)/(2n))....×sin (((n−1)π)/n)))^(1/n) =?
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt[{{n}}]{\mathrm{sin}\:\frac{\pi}{\mathrm{2}{n}}×\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{2}{n}}×\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{2}{n}}….×\mathrm{sin}\:\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}}=? \\ $$
Answered by Ar Brandon last updated on 09/Jan/22
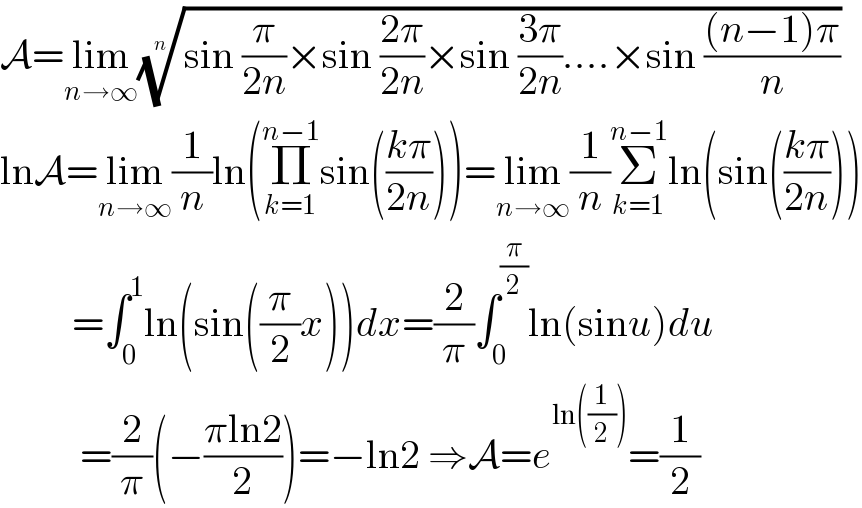
A=lim_(n→∞) ((sin (π/(2n))×sin ((2π)/(2n))×sin ((3π)/(2n))....×sin (((n−1)π)/n)))^(1/n) lnA=lim_(n→∞) (1/n)ln(Π_(k=1) ^(n−1) sin(((kπ)/(2n))))=lim_(n→∞) (1/n)Σ_(k=1) ^(n−1) ln(sin(((kπ)/(2n)))) =∫_0 ^1 ln(sin((π/2)x))dx=(2/π)∫_0 ^(π/2) ln(sinu)du =(2/π)(−((πln2)/2))=−ln2 ⇒A=e^(ln((1/2))) =(1/2)
$$\mathcal{A}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\sqrt[{{n}}]{\mathrm{sin}\:\frac{\pi}{\mathrm{2}{n}}×\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{2}{n}}×\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{2}{n}}….×\mathrm{sin}\:\frac{\left({n}−\mathrm{1}\right)\pi}{{n}}} \\ $$$$\mathrm{ln}\mathcal{A}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\mathrm{ln}\left(\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{n}}\right)\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{ln}\left(\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{n}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}{x}\right)\right){dx}=\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{u}\right){du} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\pi}\left(−\frac{\pi\mathrm{ln2}}{\mathrm{2}}\right)=−\mathrm{ln2}\:\Rightarrow\mathcal{A}={e}^{\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by qaz last updated on 09/Jan/22
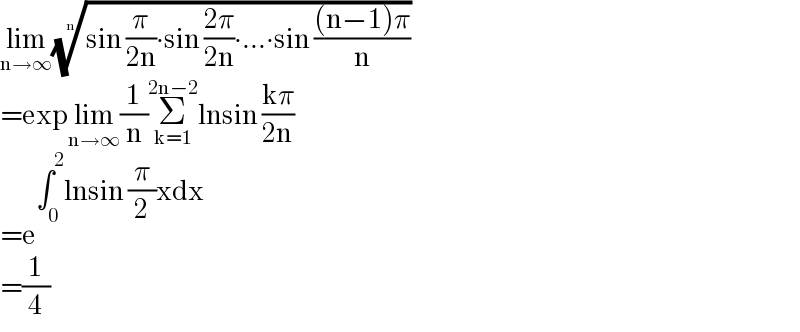
lim_(n→∞) ((sin (π/(2n))∙sin ((2π)/(2n))∙...∙sin (((n−1)π)/n)))^(1/n) =explim_(n→∞) (1/n)Σ_(k=1) ^(2n−2) lnsin ((kπ)/(2n)) =e^(∫_0 ^2 lnsin (π/2)xdx) =(1/4)
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\sqrt[{\mathrm{n}}]{\mathrm{sin}\:\frac{\pi}{\mathrm{2n}}\centerdot\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{2n}}\centerdot…\centerdot\mathrm{sin}\:\frac{\left(\mathrm{n}−\mathrm{1}\right)\pi}{\mathrm{n}}} \\ $$$$=\mathrm{exp}\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2n}−\mathrm{2}} {\sum}}\mathrm{lnsin}\:\frac{\mathrm{k}\pi}{\mathrm{2n}} \\ $$$$=\mathrm{e}^{\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{lnsin}\:\frac{\pi}{\mathrm{2}}\mathrm{xdx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *