Question Number 176808 by cortano1 last updated on 27/Sep/22
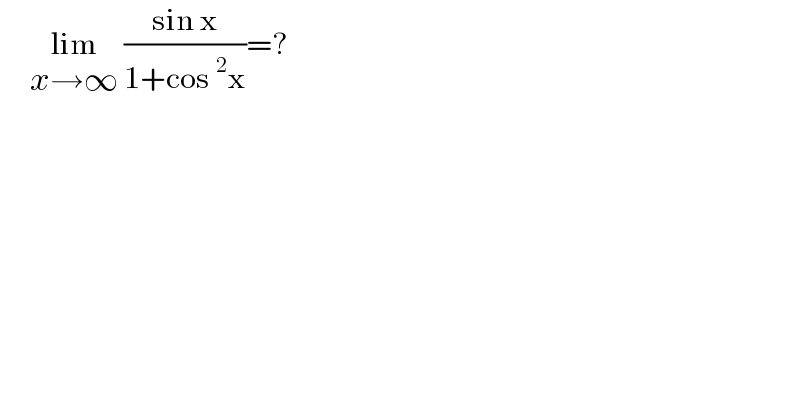
$$\:\:\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}=? \\ $$
Answered by TheHoneyCat last updated on 08/Oct/22
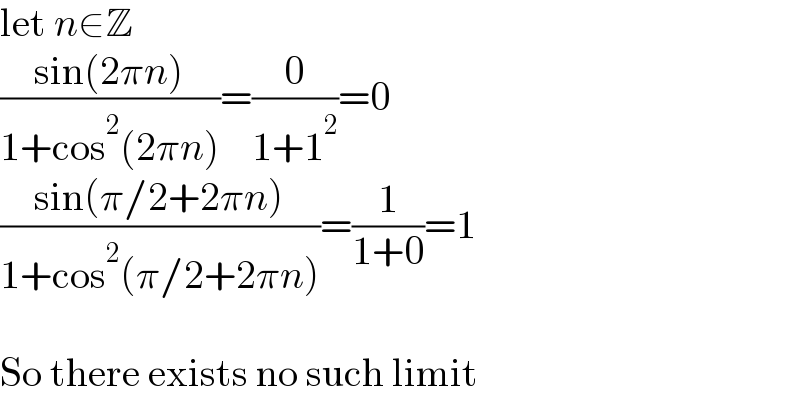
$$\mathrm{let}\:{n}\in\mathbb{Z} \\ $$$$\frac{\mathrm{sin}\left(\mathrm{2}\pi{n}\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{2}\pi{n}\right)}=\frac{\mathrm{0}}{\mathrm{1}+\mathrm{1}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{\mathrm{sin}\left(\pi/\mathrm{2}+\mathrm{2}\pi{n}\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \left(\pi/\mathrm{2}+\mathrm{2}\pi{n}\right)}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{0}}=\mathrm{1} \\ $$$$ \\ $$$$\mathrm{So}\:\mathrm{there}\:\mathrm{exists}\:\mathrm{no}\:\mathrm{such}\:\mathrm{limit} \\ $$
