Question Number 119517 by bemath last updated on 25/Oct/20
![lim_(x→∞) [ sin (x+(1/x))−sin x ] =?](https://www.tinkutara.com/question/Q119517.png)
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\:\mathrm{sin}\:\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{sin}\:{x}\:\right]\:=? \\ $$
Answered by Dwaipayan Shikari last updated on 25/Oct/20
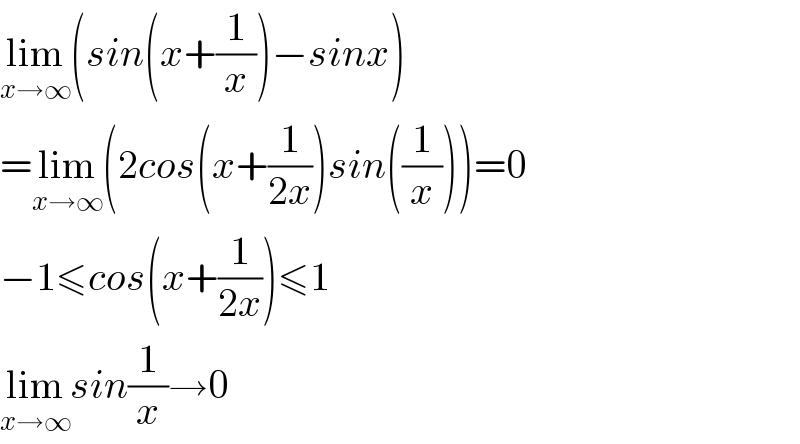
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({sin}\left({x}+\frac{\mathrm{1}}{{x}}\right)−{sinx}\right) \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{2}{cos}\left({x}+\frac{\mathrm{1}}{\mathrm{2}{x}}\right){sin}\left(\frac{\mathrm{1}}{{x}}\right)\right)=\mathrm{0} \\ $$$$−\mathrm{1}\leqslant{cos}\left({x}+\frac{\mathrm{1}}{\mathrm{2}{x}}\right)\leqslant\mathrm{1} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{sin}\frac{\mathrm{1}}{{x}}\rightarrow\mathrm{0} \\ $$
Answered by benjo_mathlover last updated on 25/Oct/20
![lim_(x→∞) [ sin xcos (1/x)+cos xsin (1/x)−sin x ] = lim_(x→∞) [ sin x(cos (1/x)−1)+cos x sin (1/x) ] [ note lim_(x→∞) cos (1/x)−1 = 0 ∧ lim_(x→∞) cos xsin (1/x) = 0 because cos x oscilates between −1 and 1 ] thus lim_(x→∞) [ sin x(cos (1/x)−1)+cos xsin (1/x) ] = 0](https://www.tinkutara.com/question/Q119525.png)
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\:\mathrm{sin}\:{x}\mathrm{cos}\:\frac{\mathrm{1}}{{x}}+\mathrm{cos}\:{x}\mathrm{sin}\:\frac{\mathrm{1}}{{x}}−\mathrm{sin}\:{x}\:\right]\:= \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\:\mathrm{sin}\:{x}\left(\mathrm{cos}\:\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)+\mathrm{cos}\:{x}\:\mathrm{sin}\:\frac{\mathrm{1}}{{x}}\:\right] \\ $$$$\left[\:{note}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{cos}\:\frac{\mathrm{1}}{{x}}−\mathrm{1}\:=\:\mathrm{0}\:\wedge\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{cos}\:{x}\mathrm{sin}\:\frac{\mathrm{1}}{{x}}\:=\:\mathrm{0}\:\right. \\ $$$$\left.{because}\:\mathrm{cos}\:{x}\:{oscilates}\:{between}\:−\mathrm{1}\:{and}\:\mathrm{1}\:\right] \\ $$$${thus}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\:\mathrm{sin}\:{x}\left(\mathrm{cos}\:\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)+\mathrm{cos}\:{x}\mathrm{sin}\:\frac{\mathrm{1}}{{x}}\:\right]\:=\:\mathrm{0} \\ $$
