Question Number 125089 by bounhome last updated on 08/Dec/20
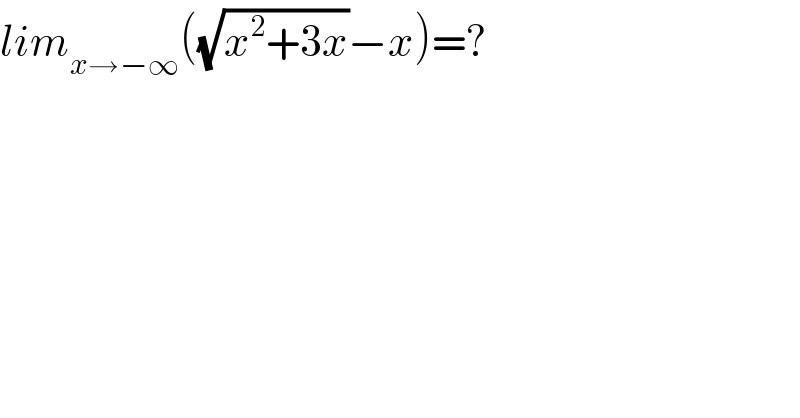
$${lim}_{{x}\rightarrow−\infty} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{3}{x}}−{x}\right)=? \\ $$
Answered by Bird last updated on 08/Dec/20
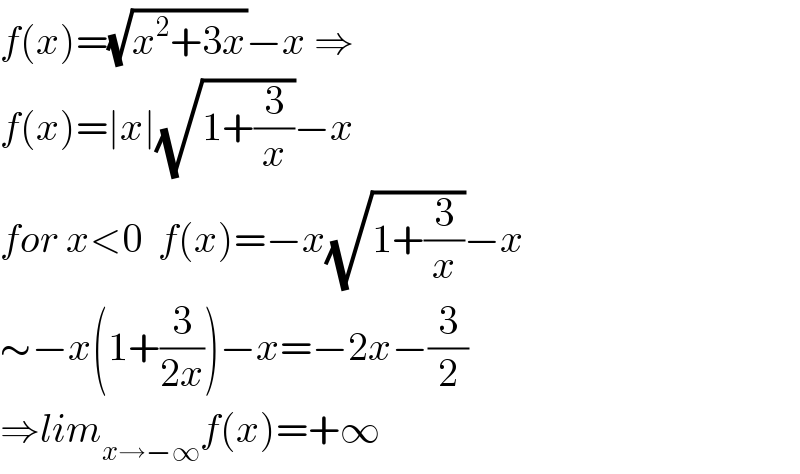
$${f}\left({x}\right)=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}{x}}−{x}\:\Rightarrow \\ $$$${f}\left({x}\right)=\mid{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{3}}{{x}}}−{x} \\ $$$${for}\:{x}<\mathrm{0}\:\:{f}\left({x}\right)=−{x}\sqrt{\mathrm{1}+\frac{\mathrm{3}}{{x}}}−{x} \\ $$$$\sim−{x}\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}{x}}\right)−{x}=−\mathrm{2}{x}−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow−\infty} {f}\left({x}\right)=+\infty \\ $$
