Question Number 127421 by Study last updated on 29/Dec/20
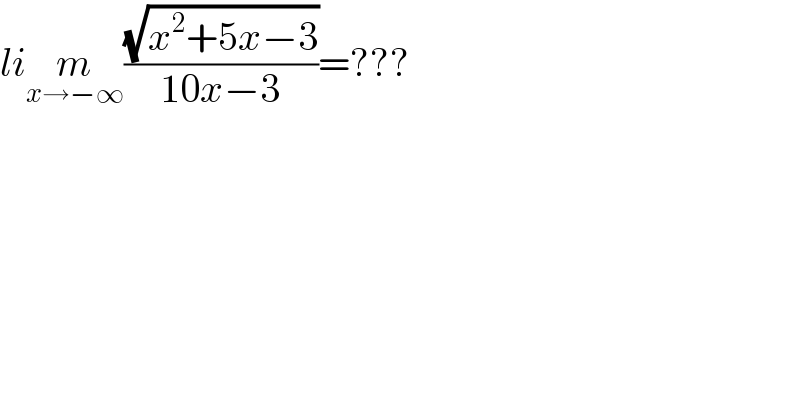
$${li}\underset{{x}\rightarrow−\infty} {{m}}\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{3}}}{\mathrm{10}{x}−\mathrm{3}}=??? \\ $$
Answered by ebi last updated on 29/Dec/20

$$\underset{{x}\rightarrow−\infty} {{lim}}\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{3}}}{\mathrm{10}{x}−\mathrm{3}} \\ $$$$=\underset{{x}\rightarrow−\infty} {{lim}}\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{3}}}{\mathrm{10}{x}−\mathrm{3}}=\underset{{x}\rightarrow−\infty} {{lim}}\frac{\sqrt{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{5}}{{x}}−\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)}}{{x}\left(\mathrm{10}−\frac{\mathrm{3}}{{x}}\right)} \\ $$$$=\underset{{x}\rightarrow−\infty} {{lim}}\frac{\mid{x}\mid\sqrt{\left(\mathrm{1}+\frac{\mathrm{5}}{{x}}−\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)}}{{x}\left(\mathrm{10}−\frac{\mathrm{3}}{{x}}\right)} \\ $$$$=\underset{{x}\rightarrow−\infty} {{lim}}\frac{−{x}\sqrt{\left(\mathrm{1}+\frac{\mathrm{5}}{{x}}−\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)}}{{x}\left(\mathrm{10}−\frac{\mathrm{3}}{{x}}\right)},\:\mid{x}\mid=\begin{cases}{{x},\:{x}\geqslant\mathrm{0}}\\{−{x},\:{x}<\mathrm{0}}\end{cases} \\ $$$$=\underset{{x}\rightarrow−\infty} {{lim}}\frac{−\sqrt{\left(\mathrm{1}+\frac{\mathrm{5}}{{x}}−\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)}}{\left(\mathrm{10}−\frac{\mathrm{3}}{{x}}\right)}=\frac{−\sqrt{\mathrm{1}+\mathrm{0}−\mathrm{0}}}{\mathrm{10}}=−\frac{\mathrm{1}}{\mathrm{10}} \\ $$
