Question Number 161867 by cortano last updated on 23/Dec/21
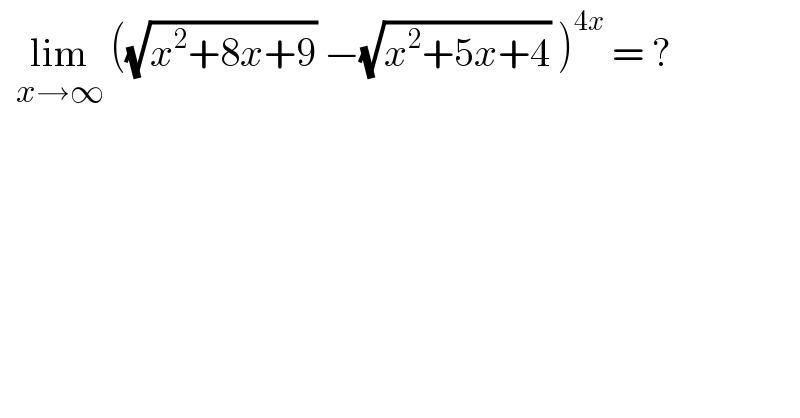
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{9}}\:−\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{4}}\:\right)^{\mathrm{4}{x}} \:=\:? \\ $$
Answered by Ar Brandon last updated on 23/Dec/21
![A=lim_(x→∞) ((√(x^2 +8x+9))−(√(x^2 +5x+4)))^(4x) =lim_(x→∞) (x(√(1+((8x+9)/x^2 )))−x(√(1+((5x+4)/x^2 ))))^(4x) =lim_(x→∞) (x(1+((8x+9)/(2x^2 )))−x(1+((5x+4)/(2x^2 ))))^(4x) =lim_(x→∞) (x(((3x+5)/(2x^2 ))))^(4x) =lim_(x→∞) (((3x+5)/(2xsgn(x))))^(4x) lnA=lim_(x→∞) 4xln(((3x+5)/(2x)))=lim_(x→∞) 4x[ln((3/2))+ln(1+(5/(3x)))] =lim_(x→∞) 4x(ln((3/2))+(5/(3x)))=lim_(x→∞) 4xln((3/2))→∞ ⇒A→_(x→∞) ∞](https://www.tinkutara.com/question/Q161869.png)
$$\mathcal{A}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{9}}−\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{4}}\right)^{\mathrm{4}{x}} \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({x}\sqrt{\mathrm{1}+\frac{\mathrm{8}{x}+\mathrm{9}}{{x}^{\mathrm{2}} }}−{x}\sqrt{\mathrm{1}+\frac{\mathrm{5}{x}+\mathrm{4}}{{x}^{\mathrm{2}} }}\right)^{\mathrm{4}{x}} \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({x}\left(\mathrm{1}+\frac{\mathrm{8}{x}+\mathrm{9}}{\mathrm{2}{x}^{\mathrm{2}} }\right)−{x}\left(\mathrm{1}+\frac{\mathrm{5}{x}+\mathrm{4}}{\mathrm{2}{x}^{\mathrm{2}} }\right)\right)^{\mathrm{4}{x}} \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({x}\left(\frac{\mathrm{3}{x}+\mathrm{5}}{\mathrm{2}{x}^{\mathrm{2}} }\right)\right)^{\mathrm{4}{x}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{3}{x}+\mathrm{5}}{\mathrm{2}{xsgn}\left({x}\right)}\right)^{\mathrm{4}{x}} \\ $$$$\mathrm{ln}\mathcal{A}=\underset{{x}\rightarrow\infty} {\mathrm{lim}4}{x}\mathrm{ln}\left(\frac{\mathrm{3}{x}+\mathrm{5}}{\mathrm{2}{x}}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}4}{x}\left[\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{3}{x}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}4}{x}\left(\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\frac{\mathrm{5}}{\mathrm{3}{x}}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}4}{x}\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\rightarrow\infty \\ $$$$\Rightarrow\mathcal{A}\underset{{x}\rightarrow\infty} {\rightarrow}\infty \\ $$
