Question Number 164266 by naka3546 last updated on 15/Jan/22
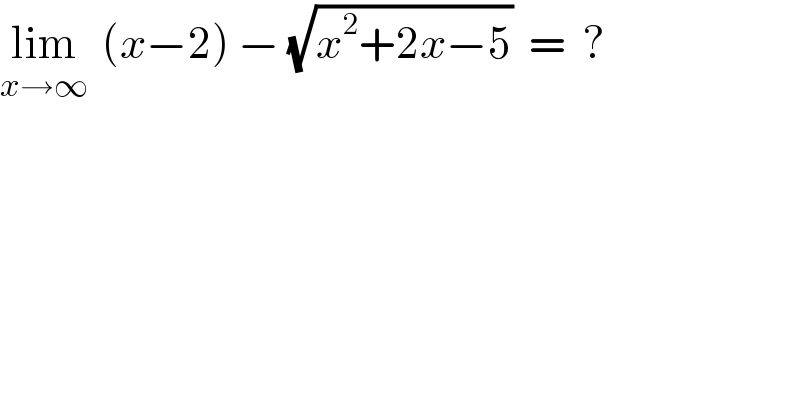
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\left({x}−\mathrm{2}\right)\:−\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{5}}\:\:=\:\:? \\ $$
Answered by ajfour last updated on 15/Jan/22
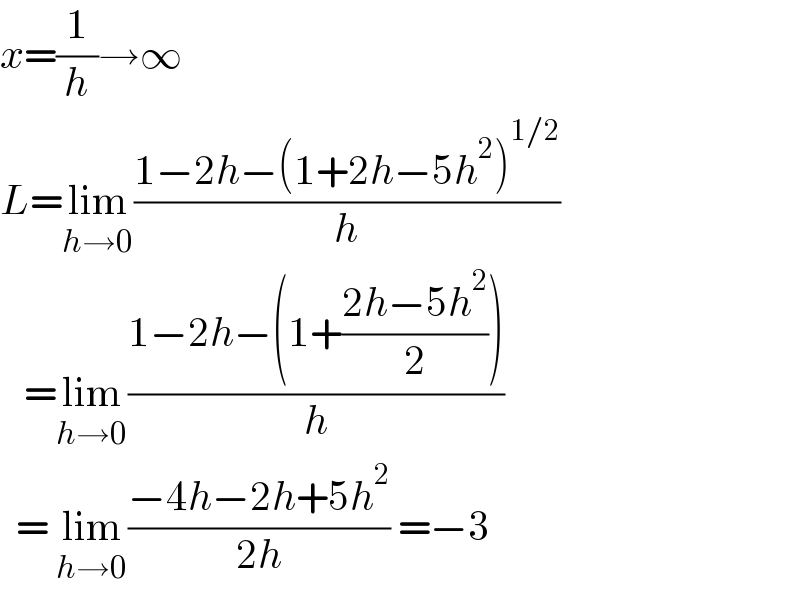
$${x}=\frac{\mathrm{1}}{{h}}\rightarrow\infty \\ $$$${L}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{2}{h}−\left(\mathrm{1}+\mathrm{2}{h}−\mathrm{5}{h}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} }{{h}} \\ $$$$\:\:\:=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{2}{h}−\left(\mathrm{1}+\frac{\mathrm{2}{h}−\mathrm{5}{h}^{\mathrm{2}} }{\mathrm{2}}\right)}{{h}} \\ $$$$\:\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{4}{h}−\mathrm{2}{h}+\mathrm{5}{h}^{\mathrm{2}} }{\mathrm{2}{h}}\:=−\mathrm{3} \\ $$
Commented by naka3546 last updated on 15/Jan/22
$${Thank}\:\:{you},\:\:{sir}. \\ $$
Answered by cortano1 last updated on 16/Jan/22
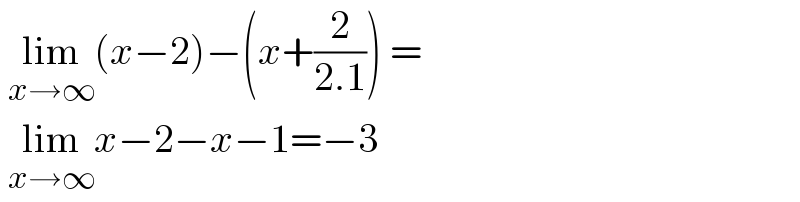
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({x}−\mathrm{2}\right)−\left({x}+\frac{\mathrm{2}}{\mathrm{2}.\mathrm{1}}\right)\:= \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{x}−\mathrm{2}−{x}−\mathrm{1}=−\mathrm{3} \\ $$
Commented by naka3546 last updated on 16/Jan/22
$${thank}\:\:{you},\:\:{sir}. \\ $$
